Voorbeeld 1 Het volgende stelsel van lineaire differentiaalvergelijkingen

$$\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -2x+ y\\[0.25cm] \frac{\dd y}{\dd t} &= 2x - y\end{aligned}\right.$$ heeft oneindig veel evenwichten, namelijk alle punten op de rechte lijn met vergelijking $y=2x$. Want dan geldt dat $\dfrac{\dd x}{\dd t}=0$ en $\dfrac{\dd x}{\dd t}=0$. Je ziet ook door optellen van beide GDVs in dat $$\frac{\dd x}{\dd t}+\frac{\dd y}{\dd t}=0$$ en dus $$\frac{\dd(x+y)}{\dd t}=0$$ oftewel $$x+y=\text{constante}$$ Dit betekent dat elk beginwaardeprobleem met beginwaarden $x_0$ en $y_0$ oplossingen heeft zodanig dat de parameterkromme $t\mapsto \bigl(x(t), y(t)\bigr)$ een halve rechte lijn is met vergelijking $y=-x+x_0+y_0$. Voor grote $t$ nadert deze parameterkromme het punt $\bigl(\tfrac{1}{3}(x_0+y_0),\tfrac{2}{3}(x_0+y_0)\bigr)$. Alle evenwichten voor dit stelsel van differentiaalvergelijkingen zijn aantrekkend. In onderstaand richtingsveld, met daarin enkele oplossingskrommen in het fasevlak getekend, zijn bovenstaande bevindingen te herkennen.

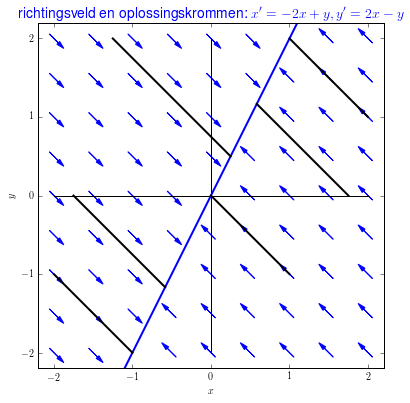
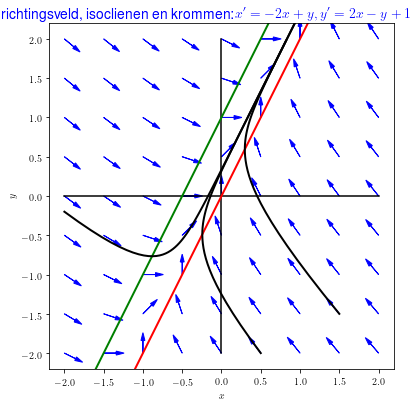
Voorbeeld 2 Het volgende stelsel van lineaire differentiaalvergelijkingen

$$\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -2x+ y\\[0.25cm] \frac{\dd y}{\dd t} &= 2x - y+1\end{aligned}\right.$$ lijkt op dat van het vorige voorbeeld, maar verschilt enkel in de tweede vergelijking waarin een constante term is toegevoegd. Er zijn nu helemaal geen evenwichten. In onderstaand richtingsveld, met daarin enkele oplossingskrommen in het fasevlak getekend, zijn bovenstaande bevindingen te herkennen.

In dit diagram hebben we ook de $x$-nul-isocliene, dat wil zeggen de punten waarvoor $\dfrac{\dd x}{\dd t}=0$ oftewel waarin de pijlen verticaal lopen, getekend in de kleur rood. In groen is de $y$-nul-isocliene, dat wil zeggen de punten waarvoor $\dfrac{\dd y}{\dd t}=0$ oftewel waarin de pijlen horizontaal lopen, getekend. Deze nul-isoclienen scheiden gebieden waarin pijlen van horizontale of verticale richting veranderen. Bijvoorbeeld in dit voorbeeld lopen krommen links van de rode $x$-nul-isocliene naar rechts, en rechts van de rode $x$-nul-isocliene naar links. Krommen lopen boven de groene $y$-nul-isocliene naar beneden en onder de groene $y$-nul-isocliene naar boven. De isoclienen helpen om het verloop van krommen kwalitatief te analyseren.

De zwart-getekende krommen wekken de indruk dat oplossingskrommen een rechte lijn naderen in de loop van de tijd. Dit klopt en bewezen kan worden dat deze lijn te beschrijven is met de vergelijking $y=2x+\dfrac{1}{3}$ en dat deze lijn zelf ook een oplossingskromme is.

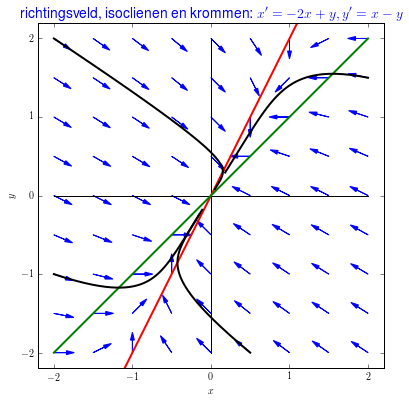
Voorbeeld 3 Het volgende stelsel van lineaire differentiaalvergelijkingen

$$\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -2x+ y\\[0.25cm] \frac{\dd y}{\dd t} &= x - y\end{aligned}\right.$$ lijkt op dat van het vorige voorbeeld, maar verschilt enkel in de tweede vergelijking waarin een coëfficiënt gewijzigd is van $2$ naar $1$. Er zijn nu precies één evenwicht, namelijk de oorsprong van het assenstelsel.

In onderstaand richtingsveld staan enkele oplossingskrommen in het fasevlak getekend en ze lopen allemaal in de richting van het evenwicht. Het betreft dus een aantrekkend evenwicht. In het vectorveld hebben we ook de $x$-nul-isocliene, dat wil zeggen de punten waarvoor $\dfrac{\dd x}{\dd t}=0$ oftewel waarin de pijlen verticaal lopen, getekend in de kleur rood. In groen is de $y$-nul-isocliene, dat wil zeggen de punten waarvoor $\dfrac{\dd y}{\dd t}=0$ oftewel waarin de pijlen horizontaal lopen, getekend. Deze nul-isoclienen scheiden gebieden waarin pijlen van horizontale of verticale richting veranderen. Bijvoorbeeld in dit voorbeeld lopen krommen links van de rode $x$-nul-isocliene naar rechts, en rechts van de rode $x$-nul-isocliene naar links. Krommen lopen boven de groene $y$-nul-isocliene naar beneden en onder de groene $y$-nul-isocliene naar boven. De isoclienen helpen om het verloop van krommen kwalitatief te analyseren en te begrijpen dat het evenwicht $(x,y)=(0,0)$ aantrekkend is.

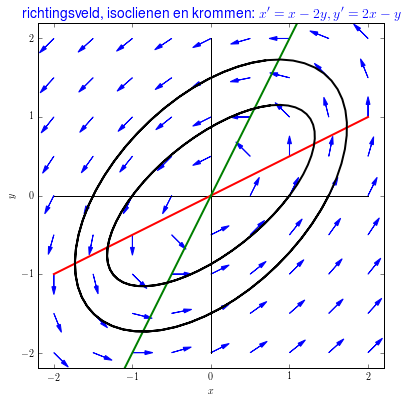
Voorbeeld 4 Het volgende stelsel van lineaire differentiaalvergelijkingen

$$\left\{\begin{aligned} \frac{\dd x}{\dd t} &= x-2y\\[0.25cm] \frac{\dd y}{\dd t} &= 2x-y\end{aligned}\right.$$ lijkt wel op het laatste voorbeeld in de zin dat er precies één evenwicht is, namelijk de oorsprong van het assenstelsel. Ook verschilt het stelsel alleen van het eerste voorbeeld in de eerste vergelijking. In onderstaand richtingsveld staan enkele oplossingskrommen in het fasevlak getekend en ze lopen allemaal linksom, tegen de wijzers van de klok in, langs een ellips. Het evenwicht $(0,0)$ is zelf een oplossing waar omheen oplossingskrommen in het fasevlak lopen.

In het richtingsveld hebben we ook de $x$-nul-isocliene, dat wil zeggen de punten waarvoor $\dfrac{\dd x}{\dd t}=0$ oftewel waarin de pijlen verticaal lopen, getekend in de kleur rood. In groen is de $y$-nul-isocliene, dat wil zeggen de punten waarvoor $\dfrac{\dd y}{\dd t}=0$ oftewel waarin de pijlen horizontaal lopen, getekend. Deze nul-isoclienen scheiden gebieden waarin pijlen van horizontale of verticale richting veranderen. Bijvoorbeeld in dit voorbeeld lopen krommen links van de rode $x$-nul-isocliene naar rechts, en rechts van de rode $x$-nul-isocliene naar links. Krommen lopen boven de groene $y$-nul-isocliene naar beneden en onder de groene $y$-nul-isocliene naar boven. De isoclienen helpen om het verloop van krommen kwalitatief te analyseren.