We gaan nog zien hoe we m.b.v. wiskundige software of interactieve computersimulaties een faseportret en oplossingskrommen kunnen tekenen. Maar je kunt ook een kwalitatieve analyse uitvoeren waarin je alleen maar schetst in welke richting een oplossingskromme in een punt in het fasevlak grofweg zou lopen.

Als voorbeeld bekijken we het stelsel

$$\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -2x+ y\\[0.25cm] \frac{\dd y}{\dd t} &= x -2 y\end{aligned}\right.$$ Allereerst bekijk je de $x$-nul-isoclienen en $y$-nul-isoclienen, dat wil zeggen de punten in het $y$-$x$ vlak waarin $\frac{\dd x}{\dd t}=0$ respectievelijk $\frac{\dd y}{\dd t}=0$. Deze isoclienen zijn rechte lijnen: $$\frac{\dd x}{\dd t} =0\iff y=2x\qquad \text{en}\qquad \frac{\dd y}{\dd t}=0\iff y=\frac{1}{2}x$$ Deze rechte lijnen scheiden in het fasevlak gebieden waarin oplossingskrommen kwalitatief in een andere richting lopen: bijvoorbeeld lopen in dit voorbeeld krommen links van de $x$-nul-isocliene naar rechts $(\frac{\dd x}{\dd t}>0)$ en rechts van de $x$-nul-isocliene naar links $(\frac{\dd x}{\dd t}<0)$; krommen boven de $y$-nul-isocliene lopen naar beneden $(\frac{\dd y}{\dd t}<0)$ en krommen beneden de $y$-nul-isocliene lopen naar boven $(\frac{\dd y}{\dd t}>0)$. Dit is ook wat je ziet in onderstaand computer-gegenereerd faseportret, waarin de rode lijn de $x$-nul-isocliene is en de groene lijn de $y$-nul-isocliene is.

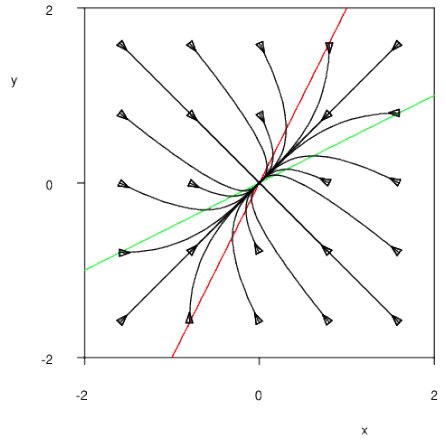
In onderstaand diagram hebben we weer de nul-isoclienen getekend maar geen oplossingskrommen. In plaats hiervan hebben we met pijlen alleen maar de richtingen aangegeven waarin een oplossingskromme in een punt zou gaan qua $x$- en $y$-verandering. De resultante vectoren geeft het richtingsveld.

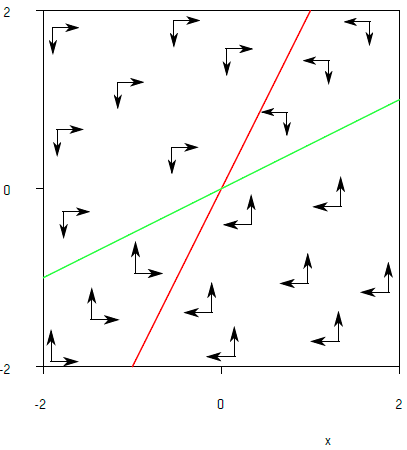
Laten we in meer detail naar bovenstaand diagram met separate $x$- en $y$-richtingen kijken, en niet naar resultante vectoren, dan zijn er vier gevallen te onderscheiden.

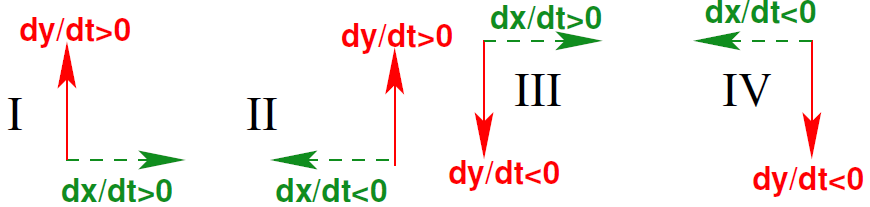
De vier gevallen zijn:

1. $x$ en $y$ stijgen allebei
2. $x$ daalt en $y$ stijgt
3. $x$ stijgt en $y$ daalt
4. $x$ en $y$ dalen allebei

De eerste twee gevallen I en II worden gescheiden door de $x$-nul-isoclienen en de gevallen I en III worden gescheiden door de $y$-nul-isoclienen. Maar de $x$-nul-isoclienen scheiden ook gevallen III en IV. Evenzo scheiden de $y$-nul-isoclienen ook gevallen II en IV.

Verder geldt dat de richting op de lijn van $x$-nul-isoclienen verticaal is en op de lijn van $y$-nul-isoclienen horizontaal is.

Tot slot merken we nog op dat alle richtingen in het diagram gericht zijn op het evenwicht $(0,0)$: alle oplossing lopen dus richting de oorsprong. Met andere woorden: $(0,0)$ is een aantrekkend evenwicht in dit voorbeeld.