Repelling equilibrium $$\left\{\begin{aligned} \frac{\dd x}{\dd t} &= 2x+ y\\[0.25cm] \frac{\dd y}{\dd t} &=x+2 y\end{aligned}\right.$$ The $x$-nullcline is the red line $y=-2x$ and the $y$-nullcline is the green line $y=-\frac{1}{2}x$. The phase portrait and diagram of directions are as follows:

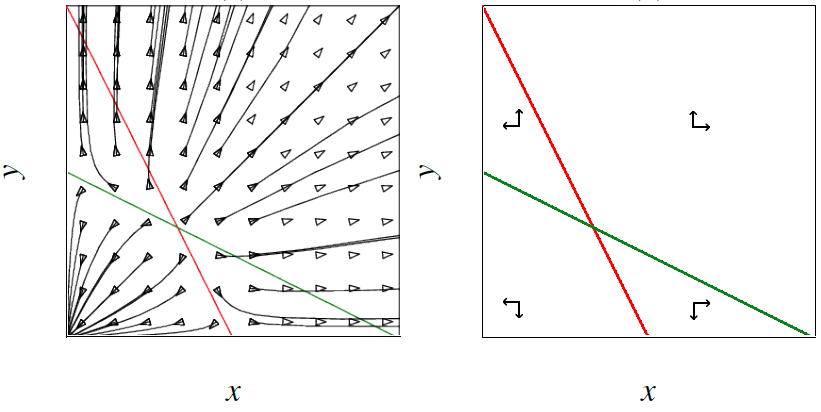
All directions are away from the equilibrium: so this is a repelling equilibrium.

Attracting equilibrium $$\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -2x-y\\[0.25cm] \frac{\dd y}{\dd t} &= -x-2 y\end{aligned}\right.$$ The $x$-nullcline is the red line $y=2x$ and the $y$-nullcline is the green line $y=\frac{1}{2}x$. The phase portrait and the diagram of directions are as follows:

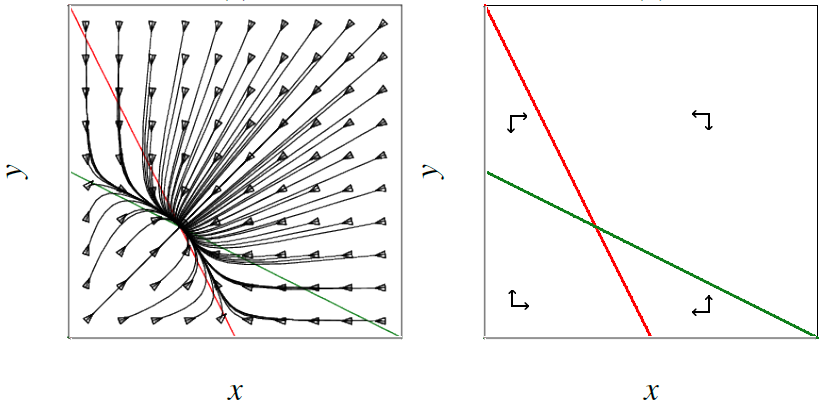
All directions are towards the equilibrium: so this is an attracting equilibrium.

Saddle point: an attracting and repelling direction $$\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -x-y\\[0.25cm] \frac{\dd y}{\dd t} &= -2x-y\end{aligned}\right.$$ The $x$-nullcline is the red line $y=-x$ and the $y$-nullcline is the green line $y=-2x$. The phase portrait and the diagram of directions are as follows:

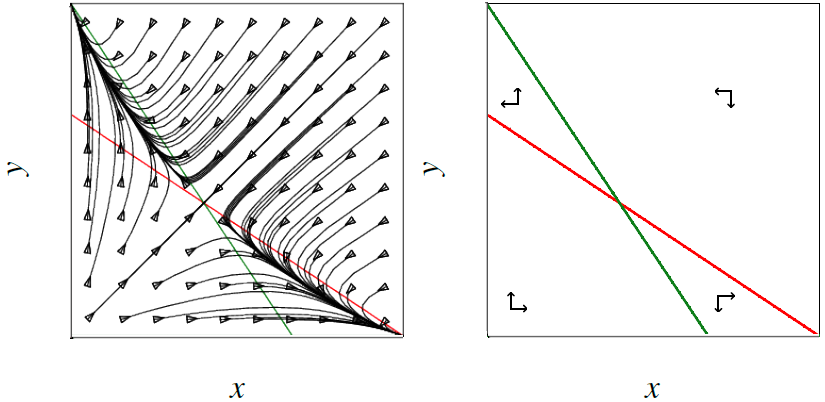
The directions are on the lower-left and upper- right side of the phase plane towards the equilibrium, but on the upper-left and the lower-right side of the phase plane away from the equilibrium. The equilibrium therefore has both a stable and unstable direction: it is a saddle point.

Inward spiral $$\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -x+2y\\[0.25cm] \frac{\dd y}{\dd t} &= -2x-y\end{aligned}\right.$$ The $x$-nullcline is the red line $y=\frac{1}{2}x$ and the $y$-nullcline is the green line $y=-2x$. The phase portrait and the diagram of directions are as follows::

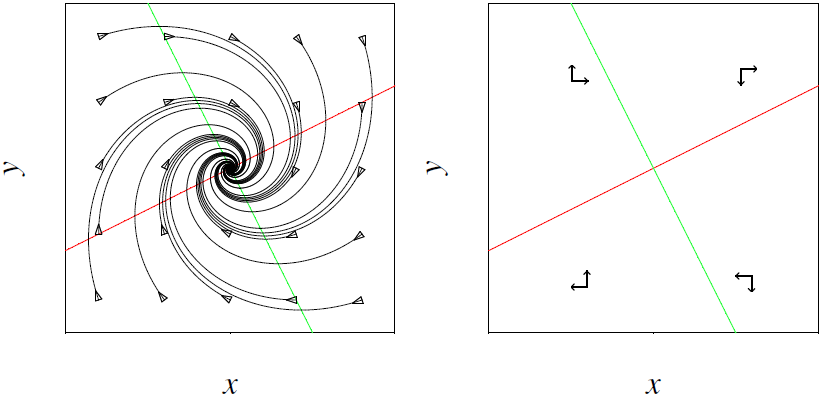
The directions indicate a rotational movement about an equilibrium but whether this is spiralling inwardly, spirals outwardly, or forms a periodic orbit about the equilibrium cannot be inferred from the directions.