Systems of differential equations: Linear systems of differential equations
Pencil-and-paper assignments: a qualitative study of stability
Task 1 Construct a qualitative phase portrait and determine herewith the nature of the equilibrium for the following linear system of differential equations \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -4x+ 2y\\[0.2cm] \frac{\dd y}{\dd t} &= x -2y\end{aligned}\right.\]
Solution You find the \(x\)-nullcline by setting \(\dfrac{\dd x}{\dd t}\) equal to \(0\): in this case \(-4x+2y=0\), i.e. \(y=2x\). This is an equation of a straight line through the origin with slope \(2\).
To the right of the line \(y=2x\) it is true that \(-4x+ 2y<0\) (take for example a point with the positive horizontal coordinate and vertical coordinate equal to \(0\)). So , on the right-hand side of this line it is true that \(\dfrac{\dd x}{\dd t}<0\) and you can draw horizontal arrows pointing to the left. On the left-hand side of the line it is opposite and you can draw horizontal arrows pointing to the right.
You find the \(y\)-nullcline by setting \(\dfrac{\dd y}{\dd t}\) equal to \(0\): in this case \(x-2y=0\), i.e. \(y=\tfrac{1}{2}x\). This is an equation of a straight line through the origin with slope \(\tfrac{1}{2}\).
Above the line \(y=\tfrac{1}{2}x\) it is true that \(x-2y<0\) (take for example a point with positive vertical coordinate and the horizontal coordinate equal to \(0\)). So above this line it is true that \(\dfrac{\dd y}{\dd t}<0\) and you can draw vertical arrows pointing downward. it is opposite and you can draw vertical arrows pointing upward.
Equilibria are the points of intersection of the two nullclines and that is, in this case, only the origin of the coordinate system.
All this gives the following diagram of directions:
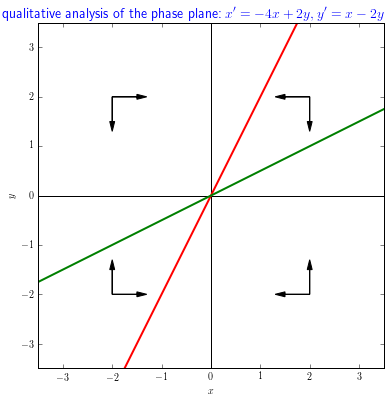
All the arrows are oriented so that they are more or less pointing in the direction of the equilibrium \((0,0)\). This is an attracting equilibrium.
Task 2 Construct a qualitative phase portrait and determine herewith the nature of the equilibrium for the following linear system of differential equations \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= x-y\\[0.2cm] \frac{\dd y}{\dd t} &= x-2y\end{aligned}\right.\]
Solution You find the \(x\)-nullcline by setting \(\dfrac{\dd x}{\dd t}\) equal to \(0\): in this case \(x-y=0\), i.e. \(y=x\). This is an equation of a straight line through the origin with slope \(1\).
To the right of the line \(y=x\) it is true that \(-x-y>0\) (take for example a point with the positive horizontal coordinate and vertical coordinate equal to \(0\)). So , on the right-hand side of this line it is true that \(\dfrac{\dd x}{\dd t}>0\) and you can draw horizontal arrows pointing to the right. On the left-hand side of the line it is opposite and you can draw horizontal arrows pointing to the left.
You find the \(y\)-nullcline by setting \(\dfrac{\dd y}{\dd t}\) equal to \(0\): in this case \(x-2y=0\), i.e. \(y=\tfrac{1}{2}x\). This is an equation of a straight line through the origin with slope \(\tfrac{1}{2}\).
Above the line \(y=\tfrac{1}{2}x\) it is true that \(x-2y<0\) (take for example a point with positive vertical coordinate and the horizontal coordinate equal to \(0\)). So above this line it is true that \(\dfrac{\dd y}{\dd t}<0\) and you can draw vertical arrows pointing downward. it is opposite and you can draw vertical arrows pointing upward.
Equilibria are the points of intersection of the two nullclines and that is, in this case, only the origin of the coordinate system.
All this gives the following diagram of directions:
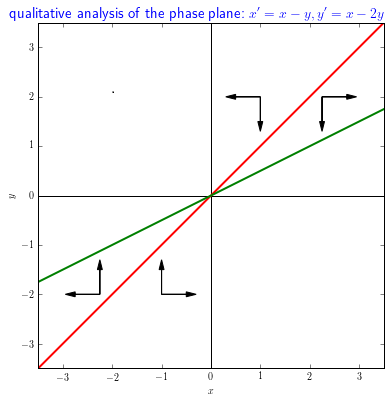
In the diagram, two directions toward and away of the equilibrium \((0,0)\) can be recognized: vertical arrows directed towards the equilibrium and horizontal arrows directed away from the equilibrium. The equilibrium is a saddle point.
