Stelsels van differentiaalvergelijkingen: Lineaire stelsels van differentiaalvergelijkingen
Pen-en-papier opgaven: een kwalitatief onderzoek naar stabiliteit
Opdracht 1 Maak een kwalitatief faseportret en bepaal hiermee de aard van het evenwicht voor het volgende stelsel van differentiaalvergelijkingen \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -4x+ 2y\\[0.25cm] \frac{\dd y}{\dd t} &= x -2y\end{aligned}\right.\]
Uitwerking De \(x\)-nul-isocliene vind je door \(\dfrac{\dd x}{\dd t}\) gelijk aan \(0\) te stellen: in dit geval \(-4x+2y=0\) oftewel \(y=2x\). Dit is een vergelijking van een rechte lijn door de oorsprong met helling \(2\) .
Rechts van de lijn \(y=2x\) geldt dat \(-4x+ 2y<0\) (neem bijvoorbeeld een punt met positieve horizontale coördinaat en verticale coördinaat gelijk aan \(0\)). Dus rechts van deze lijn is \(\dfrac{\dd x}{\dd t}<0\) en kun je horizontale pijlen naar links tekenen. Links van de lijn is het precies andersom en kun je horizontale pijlen naar rechts tekenen.
De \(y\)-nul-isocliene vind je door \(\dfrac{\dd y}{\dd t}\) gelijk aan \(0\) te stellen: in dit geval \(x-2y=0\) oftewel \(y=\tfrac{1}{2}x\). Dit is een vergelijking van een rechte lijn door de oorsprong met helling \(\tfrac{1}{2}\).
Boven de lijn \(y=\tfrac{1}{2}x\) geldt dat \(x-2y<0\) (neem bijvoorbeeld een punt met positieve verticale coördinaat en horizontale coördinaat gelijk aan \(0\)). Dus boven deze lijn is \(\dfrac{\dd y}{\dd t}<0\) en kun je verticale pijlen naar beneden tekenen. Onder de lijn is het precies andersom en kun je verticale pijlen naar boven tekenen.
Evenwichten zijn de snijpunten van de twee nul-isoclienen en dat is in dit geval alleen de oorsprong van het assenstelsel.
Dit alles geeft het volgende richtingendiagram:
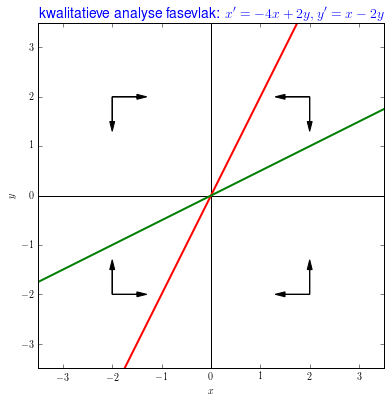
Alle pijlen zijn zo gericht dat ze min of meer wijzen in de richting van het evenwicht \((0,0)\). Dit evenwicht is dus aantrekkend.
Opdracht 2 Maak een kwalitatief faseportret en bepaal hiermee de aard van het evenwicht voor het volgende stelsel van differentiaalvergelijkingen \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= x-y\\[0.25cm] \frac{\dd y}{\dd t} &= x-2y\end{aligned}\right.\]
Uitwerking De \(x\)-nul-isocliene vind je door \(\dfrac{\dd x}{\dd t}\) gelijk aan \(0\) te stellen: in dit geval \(x-y=0\) oftewel \(y=x\). Dit is een vergelijking van een rechte lijn door de oorsprong met helling \(1\) .
Rechts van de lijn \(y=x\) geldt dat \(x-y>0\) (neem bijvoorbeeld een punt met positieve horizontale coördinaat en verticale coördinaat gelijk aan \(0\)). Dus rechts van deze lijn is \(\dfrac{\dd x}{\dd t}>0\) en kun je horizontale pijlen naar rechts tekenen. Links van de lijn is het precies andersom en kun je horizontale pijlen naar links tekenen.
De \(y\)-nul-isocliene vind je door \(\dfrac{\dd y}{\dd t}\) gelijk aan \(0\) te stellen: in dit geval \(x-2y=0\) oftewel \(y=\tfrac{1}{2}x\). Dit is een vergelijking van een rechte lijn door de oorsprong met helling \(\tfrac{1}{2}\).
Boven de lijn \(y=\tfrac{1}{2}x\) geldt dat \(x-2y<0\) (neem bijvoorbeeld een punt met positieve verticale coördinaat en horizontale coördinaat gelijk aan \(0\)). Dus boven deze lijn is \(\dfrac{\dd y}{\dd t}<0\) en kun je verticale pijlen naar beneden tekenen. Onder de lijn is het precies andersom en kun je verticale pijlen naar boven tekenen.
Evenwichten zijn de snijpunten van de twee nul-isoclienen en dat is in dit geval alleen de oorsprong van het assenstelsel.
Dit alles geeft het volgende richtingendiagram:
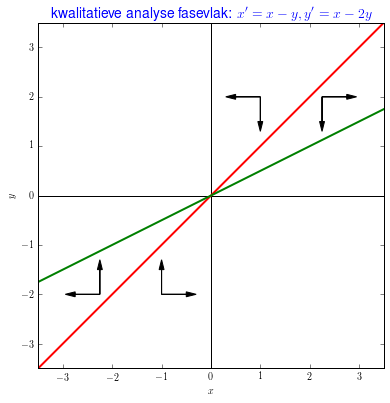
In het diagram zijn twee richtingen naar het evenwicht \((0,0)\) te herkennen: verticale pijlen er naartoe gericht en horizontale pijlen er vandaar gericht. Het evenwicht is een zadelpunt.
