Systems of differential equations: Linear systems of differential equations
 Two different real eigenvalues
Two different real eigenvalues
We consider the situation that there are two distinct real eigenvalues \(\lambda_1\) and \(\lambda_2\) of the (\(2\times 2\))-matrix \(A\) corresponding with the system \(\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y}\). Three cases can be distinguished:
- Two positive eigenvalues: \(0<\lambda_1<\lambda_2\).
- Two negative eigenvalues: \(\lambda_1<\lambda_2<0\).
- One positive and one negative eigenvalue \(\lambda_1<0<\lambda_2\).
In each of these three cases, the stability of the equilibrium \((0,0)\) is different. We always give an example.
Two positive eigenvalues Let \(\lambda_1\) and \(\lambda_2\) be positive eigenvalues, say \(0<\lambda_1<\lambda_2\), with corresponding eigenvectors \(\vec{v}_1\) and \(\vec{v}_2\). In this case \((0,0)\) is a repelling equilibrium.
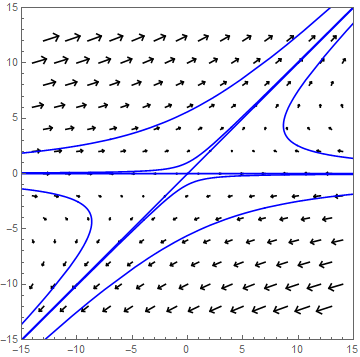
As an example we consider the system \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{with }A=\matrix{1 & 2\\ 0 & 3}\text.\] Eigenvalues and eigenvectors of \(A\) are \[\lambda_1=1\text{ with }\vec{v}_1=\cv{1\\0}\quad\text{and}\quad\lambda_2=3\text{ with }\vec{v}_2=\cv{1\\1}\text.\] The solution is \[\cv{x\\y}=c_1e^{t}\vec{v}_1+ c_2e^{3t}\vec{v}_2\] where \(c_1\) and \(c_2\) are chosen so that \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\) When \(c_2\neq 0\) we can write the solution as \(\cv{x\\y}= c_2e^{3t}\left(\vec{v}_2+ \frac{c_1}{c_2}e^{-2t}\vec{v}_1\right)\) and the solution curve approaches for large \(t\) the line though the origin with direction vector \(\vec{v}_2\).
In the figure below, called the phase portrait, several solution curves have been plotted, all of which depart from the neighbourhood of the origin. We have also drawn the vector field associated with the 2-dimensional system of differential equations. At each point \((x,y)\) in the phase portrait we can namely compute the vector \(\frac{\dd}{\dd t}\cv{x\\y}= \cv{x'\\y'}\) and draw it in the two-dimensional plane. Below this is done for points on a regular grid. The vectors give an impression of how the trajectories will be; In this case they all move further away from the origin.
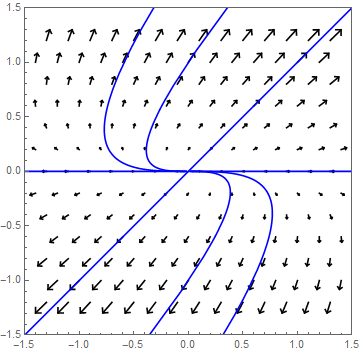
Two negative eigenvalues Let \(\lambda_1\) and \(\lambda_2\) be negative eigenvalues, say \(\lambda_1<\lambda_2<0\), with corresponding eigenvectors \(\vec{v}_1\) and \(\vec{v}_2\). In this case, \((0,0)\) is an attracting equilibrium. The trajectories are as in the above figure, but the solutions now move toward the origin.
As an example we view the system \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{met }A=\matrix{-3 & 0\\ 0 & -7}\text.\] The matching phase portrait looks like this:
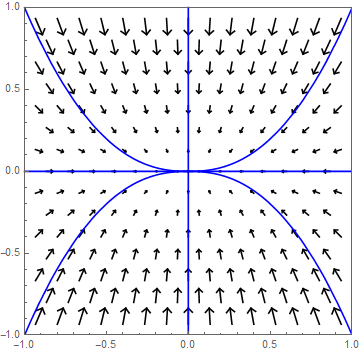
One positive and one negative eigenvalue Let \(\lambda_1\) and \(\lambda_2\) be eigenvalues with \(\lambda_1<0<\lambda_2\) and with corresponding eigenvectors \(\vec{v}_1\) and \(\vec{v}_2\), respectively. In this case, \((0,0)\) is a semi-stable equilibrium, and in particular a saddle point. When we take an initial value on the straight line through the origin with direction vector \(\vec{v}_1\), then the corresponding solution moves toward the origin. For other initial values the solutions will move away from the origin; in particular, solutions approach for large \(t\) the line through the origin with direction vector \(\vec{v}_2\).
As an example we consider the system \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{with }A=\matrix{-1 & 2\\ 0 & 1}\text.\] Eigenvalues and eigenvectors of \(A\) are \[\lambda_1=-1\text{ with }\vec{v}_1=\cv{1\\0}\quad\text{and}\quad\lambda_2=1\text{ with }\vec{v}_2=\cv{1\\1}\text.\] The solution is \[\cv{x\\y}=c_1e^{-t}\vec{v}_1+ c_2e^{t}\vec{v}_2\] where \(c_1\) and \(c_2\) are chosen so that \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\) When \(c_2\neq 0\) we can write the solution as \(\cv{x\\y}= c_2e^{t}\left(\vec{v}_2+ \frac{c_1}{c_2}e^{-2t}\vec{v}_1\right)\) and the solution curve approaches for large \(t\) the line though the origin with direction vector \(\vec{v}_2\). Several solution curves have been drawn in the following phase portrait.