Stelsels van differentiaalvergelijkingen: Lineaire stelsels van differentiaalvergelijkingen
 Twee verschillende reële eigenwaarden
Twee verschillende reële eigenwaarden
We bekijken de situatie dat er twee verschillende reële eigenwaarden \(\lambda_1\) en \(\lambda_2\) zijn van de (\(2\times 2\))-matrix \(A\) die bij het stelsel \(\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y}\) past. Er zijn 3 gevallen te onderscheiden:
- Twee positieve eigenwaarden: \(0<\lambda_1<\lambda_2\).
- Twee negatieve eigenwaarden: \(\lambda_1<\lambda_2<0\).
- Één positieve en één negatieve eigenwaarde \(\lambda_1<0<\lambda_2\).
In elk van deze drie gevallen is de stabiliteit van het evenwicht \((0,0)\) anders. We geven steeds een voorbeeld.
Twee positieve eigenwaarden Stel \(\lambda_1\) en \(\lambda_2\) zijn positieve eigenwaarden, zeg \(0<\lambda_1<\lambda_2\), met bijpassende eigenvectoren \(\vec{v}_1\) en \(\vec{v}_2\). In dit geval is \((0,0)\) een afstotend evenwicht.
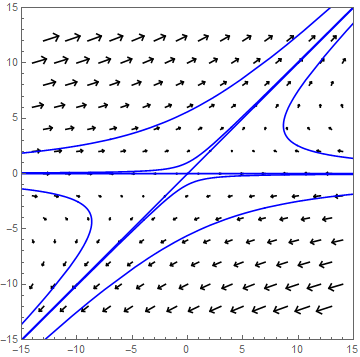
Als voorbeeld bekijken we het stelsel \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{met }A=\matrix{1 & 2\\ 0 & 3}\text.\] Eigenwaarden en eigenvectoren van \(A\) zijn \[\lambda_1=1\text{ bij }\vec{v}_1=\cv{1\\0}\quad\text{en}\quad\lambda_2=3\text{ bij }\vec{v}_2=\cv{1\\1}\text.\] De oplossing is dus \[\cv{x\\y}=c_1e^{t}\vec{v}_1+ c_2e^{3t}\vec{v}_2\] waarbij \(c_1\) en \(c_2\) zo gekozen worden dat \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\) Als \(c_2\neq 0\) dan kunnen we de oplossing schrijven als \(\cv{x\\y}= c_2e^{3t}\left(\vec{v}_2+ \frac{c_1}{c_2}e^{-2t}\vec{v}_1\right)\) en gaat de oplossingkromme voor grote \(t\) steeds dichter bij de lijn door steunpunt met richtingsvector \(\vec{v}_2\) komen.
In onderstaande figuur, het faseportret genoemd, zijn enkele oplossingskrommen getekend die allemaal vanuit de omgeving van de oorsprong vertrekken. Tevens hebben we het vectorveld horende bij het 2-dimensionale stelsel differentiaalvergelijkingen getekend. Bij elk punt \((x,y)\) in het faseportret kunnen we namelijk de vector \(\frac{\dd}{\dd t}\cv{x\\y}= \cv{x'\\y'}\) berekenen en tekenen in het vlak. Hieronder is dat voor punten op een regelmatig rooster gedaan. De vectoren geven een indruk hoe de banen zullen lopen; in dit geval steeds verder weg van de oorsprong.
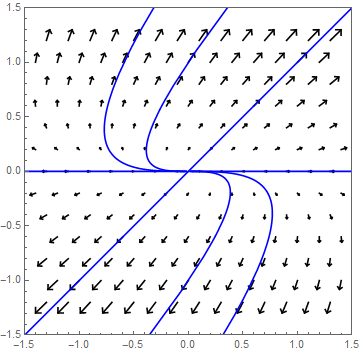
Twee negatieve eigenwaarden Stel \(\lambda_1\) en \(\lambda_2\) zijn negatieve eigenwaarden, zeg \(\lambda_1<\lambda_2<0\), met bijpassende eigenvectoren \(\vec{v}_1\) en \(\vec{v}_2\). In dit geval is \((0,0)\) een aantrekkend evenwicht. De banen zijn net als in bovenstaande figuur, maar de oplossingen lopen nu naar de oorsprong toe.
Als voorbeeld bekijken we het stelsel \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{met }A=\matrix{-3 & 0\\ 0 & -7}\text.\] Het bijpassende faseportret ziet er als volgt uit:
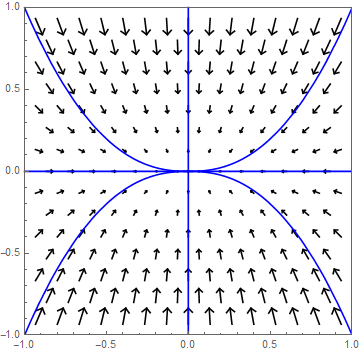
Éen positieve en één negatieve eigenwaarde Stel \(\lambda_1\) en \(\lambda_2\) zijn eigenwaarden met \(\lambda_1<0<\lambda_2\), met bijpassende eigenvectoren \(\vec{v}_1\) en \(\vec{v}_2\). In dit geval is \((0,0)\) semistabiel en in het bijzonder een zadelpunt. Nemen we een beginwaarde op de rechte lijn door de oorsprong met richtingsvector \(\vec{v}_1\), dan gaat de bijpassende oplossing naar de oorsprong toe. Voor andere beginwaarden gaan de oplossingen van de oorsprong vandaan; meer in het bijzonder komen oplossing steeds dichter bij de lijn door de oorsprong met richtingsvector \(\vec{v}_2\) te liggen.
Als voorbeeld bekijken we het stelsel \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{met }A=\matrix{-1 & 2\\ 0 & 1}\text.\] Eigenwaarden en eigenvectoren van \(A\) zijn \[\lambda_1=-1\text{ bij }\vec{v}_1=\cv{1\\0}\quad\text{en}\quad\lambda_2=1\text{ bij }\vec{v}_2=\cv{1\\1}\text.\] De oplossing is dus \[\cv{x\\y}=c_1e^{-t}\vec{v}_1+ c_2e^{t}\vec{v}_2\] waarbij \(c_1\) en \(c_2\) zo gekozen worden dat \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\) Als \(c_2\neq 0\) dan kunnen we de oplossing schrijven als \(\cv{x\\y}= c_2e^{t}\left(\vec{v}_2+ \frac{c_1}{c_2}e^{-2t}\vec{v}_1\right)\) en gaat de oplossingkromme voor grote \(t\) steeds dichter bij de lijn door de oorsprong met richtingsvector \(\vec{v}_2\) komen. In onderstaand faseportret zijn enkele oplossingskrommen getekend.