Beschouw een vectoriële grootheid \(\vec{x}(t) = \cv{x_1(t)\\ x_2(t)}\) waarvan de verandering in de tijd gegeven is door de vergelijking \(\frac{\dd\vec{x}}{\dd t} = A\,\vec{x}\) met matrix \[A =\matrix{3 & 0\\ 0 & -1}\]
-
Schrijf de vergelijking uit als een stelsel van twee lineaire differentiaalvergelijkingen.
-
Wat is de algemene formule voor de oplossing \(\vec{x}(t)\) op een willekeurig tijdstip \(t\)?
-
Wat zijn achtereenvolgens \(\vec{x}(1), \vec{x}(2)\), \(\vec{x}(4)\) en \(\vec{x}(8)\) bij \(\vec{x}(0)=\cv{1\\0}\)?
-
Hoe luiden de antwoorden bij opdracht (c) voor \(\vec{x}(0)=\cv{0\\10}\)?
- Hoe luiden de antwoorden bij opdracht (c) voor \(\vec{x}(0)=\cv{0.1\\10}\)?
-
Bij gegeven \(\vec{x}(0)\) ligt het verloop van \(x_1(t)\) en \(x_2(t)\) vast. De relatie tussen \(x_1\) en \(x_2\) kan grafisch worden weergegeven door een kromme in het \(x_2\)-\(x_1\) vlak (Je mag ook zeggen "in het \(y\)-\(x\) vlak" ).
Geef de algemene vergelijking van die krommen voor willekeurige keuze van \(\vec{x}(0)=\cv{\alpha\\\beta}\).
\(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) met \(A =\matrix{3 & 0\\ 0 & -1}\)
- \(\quad\left\{\begin{aligned} \frac{\dd x_1}{\dd t} &= 3x_1\\[0.25cm] \frac{\dd x_2}{\dd t} &= -x_2\end{aligned}\right.\)
- \(\quad\left\{\begin{aligned} x_1(t) &= c_1\cdot e^{3t}\\[0.25cm] x_2(t) &= c_2\cdot e^{-t}\end{aligned}\right.\) met constanten \(c_1\) en \(c_2\).
- \(\quad\vec{x}(0)=\cv{1\\0}\) betekent dat \(x_1(0)=1\) en \(x_2(0)=0\).
\(\quad\)Substitutie in de algemene oplossing (b) geeft: \(c_1=1\) en \(c_2=0\), en dus \(\vec{x}(t)=\cv{e^{3t}\\0}\).
\(\quad\)Dan: \(\vec{x}(1)=\cv{e^{3}\\0},\quad \vec{x}(2)=\cv{e^{6}\\0}, \quad \vec{x}(4)=\cv{e^{12}\\0}, \quad \vec{x}(8)=\cv{e^{24}\\0}\).
- \(\quad\vec{x}(0)=\cv{0\\10}\) betekent dat \(x_1(0)=0\) en \(x_2(0)=10\).
\(\quad\)Substitutie in de algemene oplossing (b) geeft: \(c_1=0\) en \(c_2=10\).
\(\quad\)Dus \(\vec{x}(t)=\cv{0\\10e^{-t}}=\cv{0\\ \frac{10}{e^{t}}}\).
\(\quad\)Dan: \(\vec{x}(1)=\cv{0\\ \frac{10}{e}},\quad \vec{x}(2)=\cv{0\\ \frac{10}{e^2}}, \quad \vec{x}(4)=\cv{0\\ \frac{10}{e^4}}, \quad \vec{x}(8)=\cv{0\\ \frac{10}{e^8}}\).
- \(\quad\vec{x}(0)=\cv{0.1\\10}\) betekent dat \(x_1(0)=0.1\) en \(x_2(0)=10\).
\(\quad\)Substitutie in de algemene oplossing (b) geeft: \(c_1=0.1\) en \(c_2=10\).
\(\quad\)Dus \(\vec{x}(t)=\cv{0.1e^{3t}\\10e^{-t}}=\cv{0.1e^{3t}\\ \frac{10}{e^{t}}}\).
\(\quad\)Dan: \(\vec{x}(1)=\cv{0.1e^3\\ \frac{10}{e}},\quad \vec{x}(2)=\cv{0.1e^6\\ \frac{10}{e^2}}, \quad \vec{x}(4)=\cv{0.1e^{12}\\ \frac{10}{e^4}}, \quad \vec{x}(8)=\cv{0.1e^{24}\\ \frac{10}{e^8}}\).
- \(\quad\vec{x}(0)=\cv{\alpha\\ \beta}\) betekent dat \(x_1(0)=\alpha\) en \(x_2(0)=\beta\).
\(\quad\)Substitutie in de algemene oplossing (b) geeft: \(c_1=\alpha\) en \(c_2=\beta\).
\(\quad\)Dus: \(\vec{x}(t)=\cv{\alpha\cdot e^{3t}\\ \beta\cdot e^{-t}}=\cv{\alpha\cdot e^{3t}\\ \frac{\beta}{e^{t}}}\).
\(\quad\)Bovenstaande formule is de parametervoorstelling van de algemene oplossing.
\(\quad\)Deze voldoet aan de volgende vergelijking: \(x_1\cdot x_2^3=\alpha\beta^3\).
\(\quad\)Elke oplossing voldoet dus aan: \(x_1\cdot x_2^3=c\) voor zekere constante \(c\).
\(\quad\)Dit is ook te zien in het onderstaande faseportret.
\(\quad\)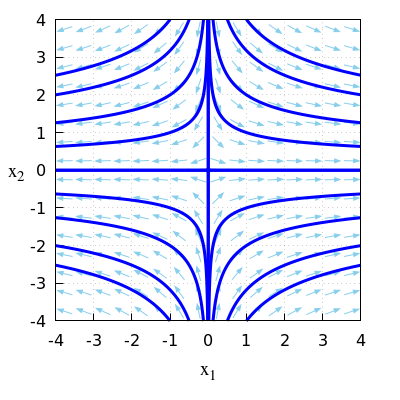
Beschouw een vectoriële grootheid \(\vec{x}(t) = \cv{x_1(t)\\ x_2(t)}\) waarvan de verandering in de tijd gegeven is door de vergelijking \(\frac{\dd\vec{x}}{\dd t} = A\,\vec{x}\) met matrix \[A =\matrix{3 & -6\\ 0 & -1}\]
-
Bereken de eigenwaarden en eigenvectoren van \(A\).
-
Wat is de algemene formule voor de oplossing \(\vec{x}(t)\) op een willekeurig tijdstip \(t\)?
-
Wat zijn achtereenvolgens \(\vec{x}(1), \vec{x}(2)\), \(\vec{x}(4)\) en \(\vec{x}(8)\) bij \(\vec{x}(0)=\cv{1\\0}\)?
-
Hoe luiden de antwoorden bij opdracht (c) voor \(\vec{x}(0)=\cv{1\\ \frac{2}{3}}\)?
- Hoe luiden de antwoorden bij opdracht (c) voor \(\vec{x}(0)=\cv{1\\ 0.666}\)?
- Hoe luiden de antwoorden bij opdracht (c) voor \(\vec{x}(0)=\cv{1\\ 0.668}\)?
-
Geef een kwalitatieve beschrijving van de algemene oplossing:
- hoe zien de banen van de oplossingen er uit? Geef een schets.
- wat is de aard van het evenwicht \((0,0)\).
\(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) met \(A = \matrix{3 & -6\\0 & -1\\}\)
- \(\quad\)De karakteristieke veelterm van \(A\) is vanwege de bovendriehoeksvorm gelijk aan \((\lambda-3)(\lambda+1)\)
\(\quad\)De eigenwaarden van \(A\) zijn nulpunten van de karakteristieke veelterm: \(3\) en \(-1\).
\(\quad\)Stel \(\cv{v_1\\ v_2}\) is een eigenvector bij eigenwaarde \(3\): \(\matrix{3 & -6\\0 & -1\\}\cdot \cv{v_1\\ v_2}=3\cv{v_1\\ v_2}\).
\(\quad\)Dan: \(\left\{\begin{aligned} 3v_1-6v_2 &= 3v_1 \\[0.25cm] -v_2 &= 3v_2\end{aligned}\right.\)
\(\quad\)Dus: \(v_2=0\) en een eigenvector bij eigenwaarde \(3\) is \(\cv{1\\0}\).
\(\quad\)Stel \(\cv{v_1\\ v_2}\) is een eigenvector bij eigenwaarde \(-1\): \(\matrix{3 & -6\\0 & -1\\}\cdot \cv{v_1\\ v_2}=-\cv{v_1\\ v_2}\).
\(\quad\)Dan: \(\left\{\begin{aligned} 3v_1-6v_2 &= -v_1 \\[0.25cm] -v_2 &= -v_2\end{aligned}\right.\)
\(\quad\)Dus: \(v_2\) is vrij te kiezen en dan moet gelden \(4v_1-6v_2=0\) oftewel \(v_2=\tfrac{2}{3}v_2\).
\(\quad\)Een eigenvector bij eigenwaarde \(-1\) (met gehele coëfficiënten) is dan \(\cv{3\\2}\).
- \(\quad\)De algemene oplossing is \[\begin{aligned}\vec{x}(t)&=\alpha\cdot e^{3t}\cdot\cv{1\\0}+ \beta\cdot e^{-t}\cdot\cv{3\\2}\\ \\ &= \cv{\alpha\cdot e^{3t}+3\beta\cdot e^{-t}\\ 2\beta\cdot e^{-t}}\end{aligned}\] \(\quad\)voor zekere constanten \(\alpha\) en \(\beta\).
- \(\quad\vec{x}(0)=\cv{1\\0}\) betekent dat \(x_1(0)=1\) en \(x_2(0)=0\).
\(\quad\)Substitutie in de algemene oplossing (b) geeft: \(\alpha=1\) en \(\beta=0\), en dus \(\vec{x}(t)=\cv{e^{3t}\\0}\).
\(\quad\)Dan: \(\vec{x}(1)=\cv{e^{3}\\0},\quad \vec{x}(2)=\cv{e^{6}\\0}, \quad \vec{x}(4)=\cv{e^{12}\\0}, \quad \vec{x}(8)=\cv{e^{24}\\0}\).
- \(\quad\)Stel \(\vec{x}(0)=\cv{1\\ \frac{2}{3}}\), dan \(\vec{x}(0)=\frac{1}{3}\cv{3\\ 2}\).
\(\quad\)Substitutie in de algemene oplossing (b) geeft: \(\alpha=0\) en \(\beta=\frac{1}{3}\).
\(\quad\)Dus: \(\vec{x}(t)=\frac{1}{3}e^{-t}\cdot\cv{3\\2}= \cv{\frac{1}{e^t}\\ \frac{2}{3e^t}}\).
\(\quad\)Dan: \(\vec{x}(1)=\cv{\frac{1}{e}\\ \frac{2}{3e}},\quad \vec{x}(2)=\cv{\frac{1}{e^2}\\ \frac{2}{3e^2}}, \quad \vec{x}(4)=\cv{\frac{1}{e^4}\\ \frac{2}{3e^4}}, \quad \vec{x}(8)=\cv{\frac{1}{e^8}\\ \frac{2}{3e^8}}\).
- \(\quad\vec{x}(0)=\cv{1\\0.666}\) is dicht in de buurt van \(\cv{1\\ \frac{2}{3}}\).
\(\quad\)Omdat \(0.666\) niet precies gelijk is aan \(\frac{2}{3}\) wijkt de oplossingskromme af,
\(\quad\)maar is in het begin (en in het verleden)dichtbij.
\(\quad\)De afwijking van \(\cv{1\\0.666}\)met \(\cv{1\\ \frac{2}{3}}\): \[\begin{aligned}\cv{1\\0.666}&=\cv{\frac{2}{3}\cdot \frac{1}{0.666}\\ \frac{2}{3}}= \cv{\frac{2}{1.998}\\ \frac{2}{3}}\\ &=\cv{\frac{2}{1.998}-1\\ 0}+\cv{1\\ \frac{2}{3}}\\ &=\cv{\frac{0.002}{1.998}\\ 0}+\cv{1\\ \frac{2}{3}}\\ &=\frac{2}{1998}\cdot\cv{1\\0}+ \cv{1\\ \frac{2}{3}}\\ &=\frac{1}{999}\cdot\cv{1\\0}+\frac{1}{3}\cdot\cv{3\\ 2}\end{aligned}\] \(\quad\)In de algemene oplossing (b) hebben we dus \(\alpha=\frac{1}{999}\) en \(\beta=\frac{1}{3}\) oftewel: \[\vec{x}(t)= \frac{1}{999}e^{3t}\cdot\cv{1\\0}+\frac{1}{3}\beta e^{-t}\cdot\cv{3\\2}\] \(\quad\)Dan: \[\begin{aligned}\vec{x}(1) &= \frac{1}{999}e^{3}\cdot\cv{1\\0}+\frac{1}{3e}\cdot\cv{3\\2} \\ \\ \vec{x}(2) &= \frac{1}{999}e^{6}\cdot\cv{1\\0}+\frac{1}{3e^2}\cdot\cv{3\\2}\\ \\ \vec{x}(4) &= \frac{1}{999}e^{12}\cdot\cv{1\\0}+\frac{1}{3e^4}\cdot\cv{3\\2}\\ \\ \vec{x}(8) &= \frac{1}{999}e^{24}\cdot\cv{1\\0}+\frac{1}{3e^8}\cdot\cv{3\\2}\approx \cv{2.65\cdot 10^7\\ 0.006}\end{aligned}\]
- \(\quad\vec{x}(0)=\cv{1\\0.668}\) is dicht in de buurt van \(\cv{1\\ \frac{2}{3}}\).
\(\quad\)Omdat \(0.668\) niet precies gelijk is aan \(\frac{2}{3}\) wijkt de oplossingskromme af,
\(\quad\)maar is in het begin (en terug in het verleden) dichtbij. De afwijking van \(\cv{1\\0.668}\) met \(\cv{1\\ \frac{2}{3}}\): \[\begin{aligned}\cv{1\\0.668}&=\cv{\frac{2}{3}\cdot \frac{1}{0.668}\\ \frac{2}{3}}= \cv{\frac{2}{2.004}\\ \frac{2}{3}}=\cv{\frac{1}{1.002}\\ \frac{2}{3}}\\ &=\cv{\frac{1}{1.002}-1\\ 0}+\cv{1\\ \frac{2}{3}}\\ &=\cv{\frac{-0.002}{1.002}\\ 0}+\cv{1\\ \frac{2}{3}}\\ &=-\frac{1}{501}\cdot\cv{1\\0}+\frac{1}{3}\cdot\cv{3\\ 2}\end{aligned}\] \(\quad\)In de algemene oplossing (b) hebben we dus \(\alpha=-\frac{1}{501}\) en \(\beta=\frac{1}{3}\) oftewel: \[\vec{x}(t)= -\frac{1}{501}e^{3t}\cdot\cv{1\\0}+\frac{1}{3}\beta e^{-t}\cdot\cv{3\\2}\] \(\quad\)Dan: \[\begin{aligned}\vec{x}(1) &= -\frac{1}{501}e^{3}\cdot\cv{1\\0}+\frac{1}{3e}\cdot\cv{3\\2} \\ \\ \vec{x}(2) &=- \frac{1}{501}e^{6}\cdot\cv{1\\0}+\frac{1}{3e^2}\cdot\cv{3\\2}\\ \\ \vec{x}(4) &= -\frac{1}{501}e^{12}\cdot\cv{1\\0}+\frac{1}{3e^4}\cdot\cv{3\\2}\\ \\ \vec{x}(8) &= -\frac{1}{501}e^{24}\cdot\cv{1\\0}+\frac{1}{3e^8}\cdot\cv{3\\2}\approx \cv{-5.29\cdot 10^7\\ 0.006}\end{aligned}\]
- \(\quad(0,0)\) is een evenwicht.
\(\quad\)Een oplossing op de lijn \(x_2=\frac{2}{3}x_1\) gaat naar het evenwicht toe.
\(\quad\)Een oplossing op de lijn \(x_2=0\) gaat van het evenwicht weg.
\(\quad\)Een oplossing die dicht bij de lijn \(x_2=\frac{2}{3}x_1\) start loopt er vandaan en gaat naar horizontale as.
\(\quad\)Het evenwicht \((0,0)\) is een zadelpunt.
\(\quad\)Dit is ook te zien in het onderstaande faseportret.
\(\quad\)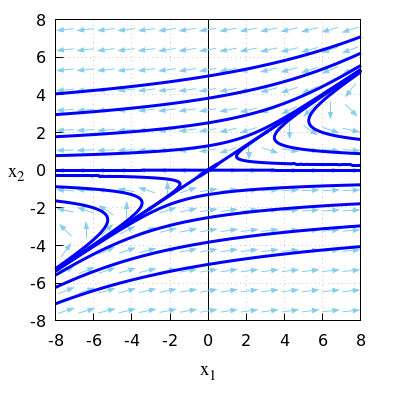
\(\quad\)Elke oplossing voldoet aan: \((2x_1-3x_2)\cdot x_2^3=c\) voor zekere constante \(c\).
 Pen-en-papier oefeningen 1
Pen-en-papier oefeningen 1




