Systems of differential equations: Linear systems of differential equations
 One real eigenvalue
One real eigenvalue
We consider the situation that the (\(2\times 2\)) matrix \(A\) corresponding with the system \(\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y}\) has one real eigenvalue \(\lambda\). Two cases can be distinguished:
- The eigenspace is two-dimensional, that is, there are two eigenvectors that are not multiples of each other.
- The eigenspace is one-dimensional, that is, eigenvectors are aligned.
The stability of the equilibrium \((0,0)\) is different in each of these two cases. We always give an example.
Twee-dimensionale eigenruimte Let \(\lambda\) be an eigenvalue with corresponding eigenvectors \(\vec{v}_1\) and \(\vec{v}_2\) that are not multiples of each other. In this case \((0,0)\) is a repelling or attracting equilibrium depending on whether the eigenvalue is positive or negative, respectively.
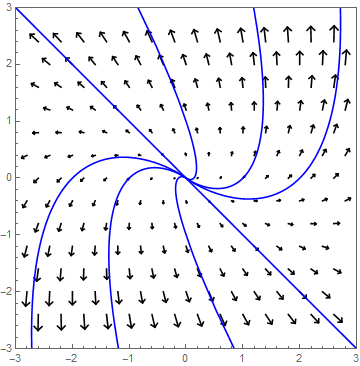
As an example we consider the system \[\frac{\dd }{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{with }A=\matrix{-1 & 0\\ 0 & -1}\text.\] Eigenvalues and eigenvectors of \(A\) are \[\lambda_1=-1\text{ with }\vec{v}_1=\cv{1\\0}\quad\text{and}\quad\lambda_2=-1\text{ with }\vec{v}_2=\cv{0\\1}\text.\] The solution is \[\cv{x\\y}=c_1e^{-t}\vec{v}_1+ c_2e^{-t}\vec{v}_2\] where \(c_1\) and \(c_2\) are chosen so that \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\). Trajectories are straight lines moving in the direction of the origin, as the following phase portrait illustrates.
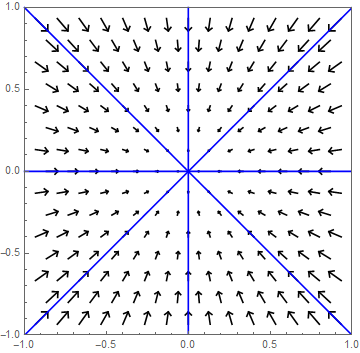
One-dimensional eigenspace Let \(\lambda\) be an eigenvalue with corresponding eigenvector \(\vec{v}\). The following method still leads to two types of solutions. As a matter of fact, there also exists a vector \(\vec{w}\) such that \((A-\lambda I)\vec{w}=\vec{v}\). The vectors \(\vec{w}\) are called generalised eigenvectors of \(A\). From the properties of \(\vec{w}\) follows (check!) that \(\cv{x\\ y}=c(\vec{v}t+\vec{w})e^{\lambda t}\) is a solution, too. The general solution is in this case given by \[\cv{x\\ y} = c_1e^{\lambda t}\vec{v}+c_2e^{\lambda t}(\vec{v}t+\vec{w})\text.\] In this case \((0,0)\) is a repelling or attracting equilibrium depending on whether the eigenvalue is positive or negative, respectively.
As a first example we consider the system \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{with }A=\matrix{-1 & 2\\ 0 & -1}\text.\] Eigenvalue and eigenvector of \(A\) is \[\lambda=-1\text{ with }\vec{v}=\cv{1\\0}\text.\] A generalised eigenvector, i.e., a solution of \((A-\lambda I)\vec{w}=\vec{v}\) is \[\vec{w}=\cv{0\\-\frac{1}{2}}\text.\] Thus the general solution is \[\cv{x\\y}=c_1e^{-t}\vec{v}+ c_2e^{-t}(t\vec{v}+\vec{w})\] where \(c_1\) and \(c_2\) are chosen so that \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\). The trajectories are curves which go in the direction of the origin, as the following phase portrait illustrates. The equilibrium is attracting.
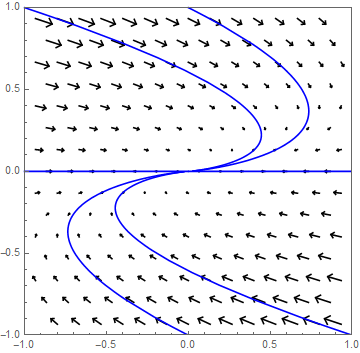
As a second example we consider the system \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{with }A=\matrix{1 & -1\\ 1 & 3}\text.\] Eigenvalue and eigenvector of \(A\) is \[\lambda=2\text{ with }\vec{v}=\cv{-1\\1}\text.\] A generalised eigenvector, i.e., a solution of \((A-\lambda I)\vec{w}=\vec{v}\) is \[\vec{w}=\cv{1\\0}\text.\] Thus the genera solution is \[\cv{x\\y}=c_1e^{2t}\vec{v}+ c_2e^{2t}(t\vec{v}+\vec{w})\] where \(c_1\) and \(c_2\) are chosen so that \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\). The trajectories are curves which go away from the origin, as the following phase portrait illustrates. The equilibrium is repelling.