Stelsels van differentiaalvergelijkingen: Lineaire stelsels van differentiaalvergelijkingen
 Eén reële eigenwaarde
Eén reële eigenwaarde
We bekijken de situatie dat er één reële eigenwaarde \(\lambda\) is van de (\(2\times 2\))-matrix \(A\) die bij het stelsel \(\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y}\) past. Er zijn 2 gevallen te onderscheiden:
- De eigenruimte is 2-dimensionaal, dat wil zegger, er zijn twee eigenvectoren die geen veelvoud van elkaar zijn.
- De eigenruimte is 1-dimensionaal, dat wil zegger, eigenvectoren liggen op één lijn.
In elk van deze twee gevallen is de stabiliteit van het evenwicht \((0,0)\) anders. We geven steeds een voorbeeld.
Twee-dimensionale eigenruimte Stel \(\lambda\) is een eigenwaarde met bijpassende eigenvectoren \(\vec{v}_1\) en \(\vec{v}_2\), die geen veelvoud van elkaar zijn. In dit geval is \((0,0)\) een afstotend of aantrekkend evenwicht al naar gelang de eigenwaarde positief of negatief is.
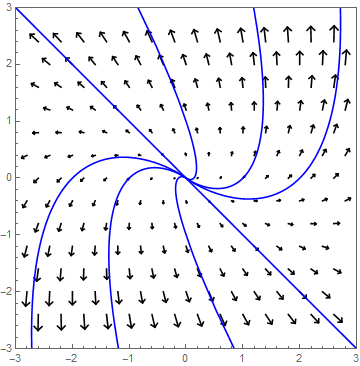
Als voorbeeld bekijken we het stelsel \[\frac{\dd }{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{met }A=\matrix{-1 & 0\\ 0 & -1}\text.\] Eigenwaarden en eigenvectoren van \(A\) zijn \[\lambda_1=-1\text{ bij }\vec{v}_1=\cv{1\\0}\quad\text{en}\quad\lambda_2=-1\text{ bij }\vec{v}_2=\cv{0\\1}\text.\] De oplossing is dus \[\cv{x\\y}=c_1e^{-t}\vec{v}_1+ c_2e^{-t}\vec{v}_2\] waarbij \(c_1\) en \(c_2\) zo gekozen worden dat \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\). De banen zijn dus rechten die in de richting van de oorsprong lopen, zoals onderstaand faseportret illustreert.
Eén-dimensionale eigenruimte Stel \(\lambda\) is een eigenwaarde met bijpassende eigenvector \(\vec{v}\). Dan geeft de volgende methode toch twee oplossingen. Er bestaat namelijk ook nog een vector \(\vec{w}\) zodanig dat \((A-\lambda I)\vec{w}=\vec{v}\). De vectoren \(\vec{w}\) heten gegeneraliseerde eigenvectoren van \(A\). Uit de eigenschappen van \(\vec{w}\) volgt (ga na!) dat \(\cv{x\\ y}=c(\vec{v}t+\vec{w})e^{\lambda t}\) ook een oplossing is. De algemene oplossing is in dit geval dus gegeven door \[\cv{x\\ y} = c_1e^{\lambda t}\vec{v}+c_2e^{\lambda t}(\vec{v}t+\vec{w})\text.\] In dit geval is \((0,0)\) een afstotend of aantrekkend evenwicht al naar gelang de eigenwaarde positief of negatief is.
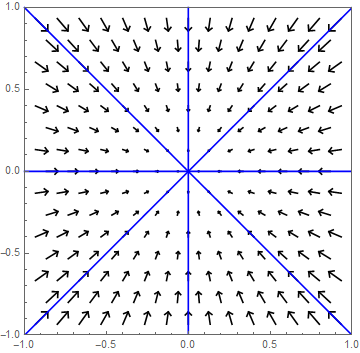
Als eerste voorbeeld bekijken we het stelsel \[\frac{\dd}{\dd t}\cv{x\\ y}=A \cv{x\\ y},\quad \text{met }A=\matrix{-1 & 2\\ 0 & -1}\text.\] Eigenwaarde en eigenvector van \(A\) is \[\lambda=-1\text{ bij }\vec{v}=\cv{1\\0}\text.\] Een gegeneraliseerde eigenvector, dat wil zeggen een oplossing van \((A-\lambda I)\vec{w}=\vec{v}\) is \[\vec{w}=\cv{0\\-\frac{1}{2}}\text.\] De oplossing is dus \[\cv{x\\y}=c_1e^{-t}\vec{v}+ c_2e^{-t}(t\vec{v}+\vec{w})\] waarbij \(c_1\) en \(c_2\) zo gekozen worden dat \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\). De banen zijn krommen die in de richting van de oorsprong lopen, zoals onderstaand faseportret illustreert.
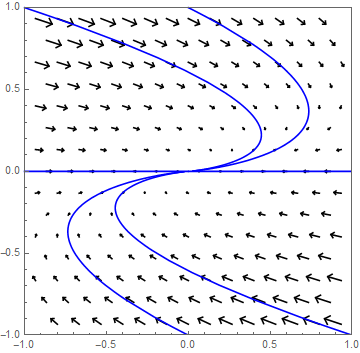
Als tweede voorbeeld bekijken we het stelsel \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{met }A=\matrix{1 & -1\\ 1 & 3}\text.\] Eigenwaarde en eigenvector van \(A\) is \[\lambda=2\text{ bij }\vec{v}=\cv{-1\\1}\text.\] Een gegeneraliseerde eigenvector, dat wil zeggen een oplossing van \((A-\lambda I)\vec{w}=\vec{v}\) is \[\vec{w}=\cv{1\\0}\text.\] De oplossing is dus \[\cv{x\\y}=c_1e^{2t}\vec{v}+ c_2e^{2t}(t\vec{v}+\vec{w})\] waarbij \(c_1\) en \(c_2\) zo gekozen worden dat \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\). De banen zijn krommen die weg van de oorsprong lopen, zoals onderstaand faseportret illustreert.