Beschouw een vectoriële grootheid \(\vec{x}(t) = \cv{x_1(t)\\ x_2(t)}\) waarvan de verandering in de tijd gegeven is door de vergelijking \(\frac{\dd\vec{x}}{\dd t} = A\,\vec{x}\) met matrix \[A =\matrix{-1 & 0\\ 1 & -1}\]
-
Bereken de eigenwaarden en eigenvectoren van \(A\).
-
Wat is de algemene formule voor de oplossing \(\vec{x}(t)\) op een willekeurig tijdstip \(t\)?
-
Wat zijn achtereenvolgens \(\vec{x}(1), \vec{x}(2)\), \(\vec{x}(4)\) en \(\vec{x}(8)\) bij \(\vec{x}(0)=\cv{3\\2}\)?
-
Hoe luiden de antwoorden bij opdracht (c) voor \(\vec{x}(0)=\cv{1\\ 0}\)? Geef de vergelijking van de baan in het \(y\)-\(x\) vlak.
- Hoe luiden de antwoorden bij opdracht (c) voor \(\vec{x}(0)=\cv{0\\ 1}\)? Geef de vergelijking van de baan in het \(y\)-\(x\) vlak.
- Geef de baanvergelijking voor willekeurige keuze \(\vec{x}(0)=\cv{\alpha \\ \beta}\)?
\(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) met \(A = \matrix{-1 & 0\\1 & -1\\}\)
- \(\quad\)De karakteristieke veelterm van \(A\) is vanwege de onderdriehoeksvorm gelijk aan \((\lambda+1)^2\)
\(\quad\)De eigenwaarden van \(A\) zijn nulpunten van de karakteristieke veelterm: \(-1\).
\(\quad\)Stel \(\cv{v_1\\ v_2}\) is een eigenvector bij eigenwaarde \(-1\): \(\matrix{-1 & 0\\1 & -1\\}\cdot \cv{v_1\\ v_2}=-\cv{v_1\\ v_2}\).
\(\quad\)Dan: \(\left\{\begin{aligned} -v_1 &= -v_1 \\[0.2cm] v_1-v_2 &= -v_2\end{aligned}\right.\)
\(\quad\)Dus: \(v_1=0\) en een eigenvector bij eigenwaarde \(-1\) (met gehele coëfficiënten) is \(\vec{v}=\cv{0\\1}\).
- \(\quad\)Een gegeneraliseerde eigenvector \(\vec{w}=\cv{w_1\\ w_2}\) bij eigenwaarde \(-1\) voldoet aan
\(\quad\)\((A-\lambda\cdot I)\vec{w}=\vec{v}\) met \(\lambda=-1\) en \(\vec{v}=\cv{0\\ 1}\)
\(\quad\)Dus: \(\matrix{0 & 0\\1 & 0\\}\cdot \cv{w_1\\ w_2}=\cv{0\\ 1}\).
\(\quad\)Dus: \(w_1=1\) en \(w_2\) is nog vrij te kiezen.
\(\quad\)Neem \(w_2=0\), dan is \(\vec{w}=\cv{1\\ 0}\) een gegeneraliseerde eigenvector.
\(\quad\)De algemene oplossing is \[\begin{aligned}\vec{x}(t)&=\beta\, e^{-t}\cdot\vec{v}+ \alpha\, e^{-t}\cdot \left(t\cdot \vec{v}+\vec{w}\right) \\ \\ &= \beta\, e^{-t}\cdot\cv{0\\1}+ \alpha\, e^{-t}\cdot \left(t\cdot \cv{0\\1}+ \cv{1\\ 0}\right)\\ \\ &= \cv{\alpha\, e^{-t}\\ \beta\, e^{-t}+\alpha\, t\, e^{-t}}\end{aligned}\] \(\quad\)voor zekere constanten \(\alpha\) en \(\beta\).
- \(\quad\vec{x}(0)=\cv{3\\2}\) betekent dat \(x_1(0)=3\) en \(x_2(0)=2\).
\(\quad\)Substitutie in de algemene oplossing (b) geeft: \(\alpha=3\) en \(\beta=2\), en dus
\(\quad\)\(\vec{x}(t)=\cv{3e^{-t}\\ 2e^{-t}+3t e^{-t}}\).
\(\quad\)Dan: \(\vec{x}(1)=\cv{3/e\\ 5/e},\quad \vec{x}(2)=\cv{3/e^2\\ 8/e^2}, \quad \vec{x}(4)=\cv{3/e^4\\ 14/e^4}, \quad \vec{x}(8)=\cv{3/e^8\\ 18/e^8}\).
- \(\quad\vec{x}(0)=\cv{1\\0}\) betekent dat \(x_1(0)=1\) en \(x_2(0)=0\).
\(\quad\)Substitutie in de algemene oplossing (b) geeft: \(\alpha=1\) en \(\beta=0\), en dus
\(\quad\)\(\vec{x}(t)=\cv{e^{-t}\\ t e^{-t}}\).
\(\quad\)Dan: \(\vec{x}(1)=\cv{1/e\\ 1/e},\quad \vec{x}(2)=\cv{1/e^2\\ 2/e^2}, \quad \vec{x}(4)=\cv{1/e\\ 4/e^4}, \quad \vec{x}(8)=\cv{1/e^8\\ 8/e^8}\).
\(\quad\)Als \(\left\{\begin{aligned} x_1 &= e^{-t}\\ x_2 &= te^{-t}\end{aligned}\right.\) dan \(\ln(x_1)=-t\) en \(x_2=t\cdot x_1\) en dus: \(x_2=-x_1\ln(x_1)\)
- \(\quad\vec{x}(0)=\cv{0\\1}\) betekent dat \(x_1(0)=0\) en \(x_2(0)=1\).
\(\quad\)Substitutie in de algemene oplossing (b) geeft: \(\alpha=0\) en \(\beta=1\). Dus:
\(\quad\)\(\vec{x}(t)=\cv{0\\ e^{-t}}\).
\(\quad\)Dan: \(\vec{x}(1)=\cv{0\\ 1/e},\quad \vec{x}(2)=\cv{0\\ 1/e^2}, \quad \vec{x}(4)=\cv{0\\ 1/e^4}, \quad \vec{x}(8)=\cv{0\\ 1/e^8}\).
\(\quad\)De baan is \(\left\{\cv{0\\y}\,\middle\vert\, y>0\right\}\).
- \(\quad\vec{x}(0)=\cv{\alpha\\ \beta}\) betekent dat \(x_1(0)=\alpha\) en \(x_2(0)=\beta\).
\(\quad\)Substitutie in de algemene oplossing (b) geeft \(\vec{x}(t)=\cv{\alpha\, e^{-t}\\ \beta\, e^{-t}+\alpha\, t\, e^{-t}}\).
\(\quad\)Als \(\left\{\begin{aligned} x_1 &= \alpha\, e^{-t}\\ x_2 &= \beta\, e^{-t}+\alpha\, t\, e^{-t}\end{aligned}\right.\) dan generiek: \(t=\ln\left(\frac{\alpha}{x_1}\right)\) en \(\alpha\cdot x_2=\beta\cdot x_1 + \alpha\cdot t\cdot x_1\).
\(\quad\)De baan heeft dan generiek de vergelijking \(\alpha \cdot x_2 =\beta\cdot x_1+\alpha\cdot x_1\cdot \ln\left(\frac{\alpha}{x_1}\right)\)
\(\quad\)'Generiek' betekent hier dat we bij logaritmen steeds uitgaan van een positief argument.
\(\quad\)We bekijken dus het geval dat \(\alpha>0\) en \(x_1>0\), en het geval dat \(\alpha<0\) en \(x_1<0\).
\(\quad\)Het geval dat \(\alpha=0, \beta>0\) is in (e) apart bekeken: de baan is de positieve verticale as.
\(\quad\)Dit is ook allemaal te zien in het onderstaande faseportret.
\(\quad\)Het evenwicht \((0,0)\) is aantrekkend.
\(\quad\)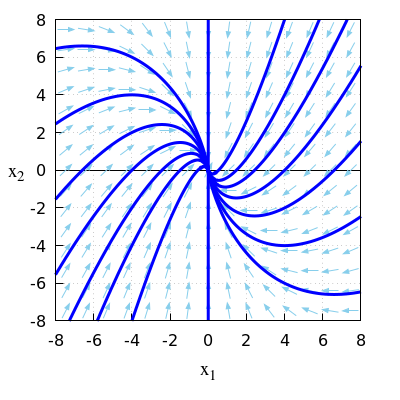
 Pen-en-papier oefeningen 2
Pen-en-papier oefeningen 2




