Systems of differential equations: Linear systems of differential equations
 Complex eigenvalues
Complex eigenvalues
We consider the following set of differential equations \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y}\quad\text{met}\quad A=\matrix{\alpha & \beta\\ -\beta & \alpha}\text{ en }\beta\neq0\] The matrix \(A\) now has two complex eigenvalues \[\lambda_1=\alpha+\beta\,\ii\quad\text{en}\quad \lambda_2=\alpha-\beta\,\ii\] There are now two special solutions: \[\cv{x\\y}=e^{\alpha t}\cv{\cos(\beta t)\\ -\sin(\beta t)}\quad\text{en}\quad e^{\alpha t}\cv{\sin(\beta t)\\ \cos(\beta t)}\] The superposition principle of the systems of linear equations indicates that all of the solutions of the following form: \[\begin{aligned}\cv{x\\y}&=c_1e^{\alpha t}\cv{\cos(\beta t)\\ -\sin(\beta t)}+c_2e^{\alpha t}\cv{\sin(\beta t)\\ \cos(\beta t)} \\ \\ &=Ae^{\alpha t}\cv{\cos(\beta t+\phi)\\ -\sin(\beta t+\phi)}\end{aligned}\] with constants \(c_1\), \(c_2\), \(A\) and \(\phi\).
There are three cases can be distinguished:
- \(\alpha<0\).
- \(\alpha=0\).
- \(\alpha>0\).
In each of these three cases, the stability of the balance \((0,0)\) else. We always give an example.
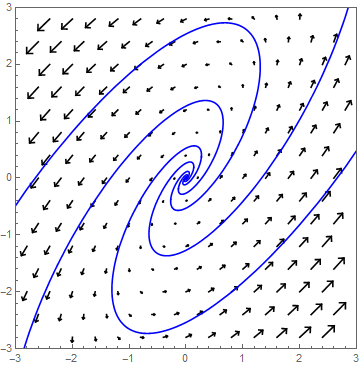
α <0 Set \(\lambda_{1,2}=\alpha\pm\beta\,\ii\) with \(\alpha<0\). Then spiraling solutions to the origin. The factor \(e^{\alpha t}\) in the general solution formula determines the amount of shrinkage.
As an example we view the system \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{met }A=\matrix{1 & -4\\ 2 & -3}\text.\] The equation for the eigenvalues is \[\det(A-\lambda I)=(1-\lambda)(-3-\lambda)- (-4)\cdot 2=\lambda^2+2\lambda+5=(\lambda+1)^2+4=0\] The eigenvalues of \(A\) with matching eigenvectors are \[\lambda_1=-1+2\ii \text{ bij }\vec{v}_1=\cv{1+\ii\\1}\quad\text{en}\quad\lambda_2=-1-2\ii\text{ bij }\vec{v}_2=\cv{1-\ii\\1}\text.\] The solution is \[\cv{x\\y}=c_1e^{-t}\cv{\cos(2t)\\ -\sin(2t)}+c_2e^{-t}\cv{\sin(2t)\\ \cos(2t)}\] which \(c_1\) and \(c_2\) are chosen so that \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\). In the following phase portrait are some solution curves drawn.
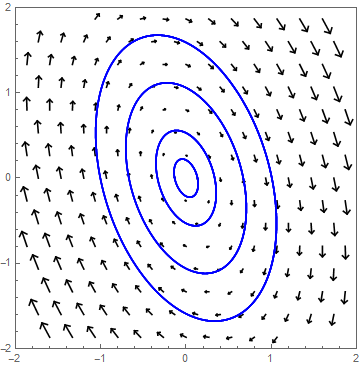
α = 0 Set \(\lambda=\pm\beta\,\ii\) with \(\alpha=0\). Then, the solutions are periodically. The jobs in the phase portrait are ellipses.
As an example we consider the system \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{met }A=\matrix{1 & 2\\ -5 & -1}\text.\] The equation for the eigenvalues is \[\det(A-\lambda I)=(1-\lambda)(-1-\lambda)- 2\cdot (-5)=\lambda^2+9=0\] The eigenvalues of \(A\) are with matching eigenvectors than \[\lambda_1=3\ii \text{ bij }\vec{v}_1=\cv{-1-3\ii\\5}\quad\text{en}\quad\lambda_2=-3\ii\text{ bij }\vec{v}_2=\cv{-1+3\ii\\5}\text.\] The solution therefore is \[\cv{x\\y}=c_1\cv{\cos(3t)\\ -\sin(3t)}+c_2\cv{\sin(3t)\\ \cos(3t)}\] wherein \(c_1\) and \(c_2\) are chosen so that \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\) In the following phase portrait are some solution curves drawn.
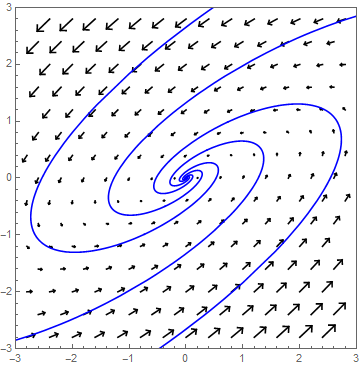
α> 0 Set \(\lambda_{1,2}=\alpha\pm\beta\,\ii\) with \(\alpha>0\). Then solutions spiraling away from the origin. The factor \(e^{\alpha t}\) in the general solution formula determines the amount of growth.
As an example we view the system \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{met }A=\matrix{3 & -2\\ 4 & -1}\text.\] The equation for the eigenvalues is \[\det(A-\lambda I)=(3-\lambda)(-1-\lambda)- (-2)\cdot 4=\lambda^2-2\lambda+5=(\lambda-1)^2+4=0\] The eigenvalues of \(A\) with matching eigenvectors are \[\lambda_1=1+2\ii \text{ bij }\vec{v}_1=\cv{1\\1+\ii}\quad\text{en}\quad\lambda_2=1-2\ii\text{ bij }\vec{v}_2=\cv{1\\1-\ii}\text.\] The solution is \[\cv{x\\y}=c_1e^{t}\cv{\cos(2t)\\ -\sin(2t)}+c_2e^{t}\cv{\sin(2t)\\ \cos(2t)}\] which \(c_1\) and \(c_2\) are chosen so that \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\). In the following phase portrait are some solution curves drawn.