Stelsels van differentiaalvergelijkingen: Lineaire stelsels van differentiaalvergelijkingen
 Complexe eigenwaarden
Complexe eigenwaarden
We bekijken het volgende stelsel differentiaalvergelijkingen \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y}\quad\text{met}\quad A=\matrix{\alpha & \beta\\ -\beta & \alpha}\text{ en }\beta\neq0\] De matrix \(A\) heeft nu twee complexe eigenwaarden \[\lambda_1=\alpha+\beta\,\ii\quad\text{en}\quad \lambda_2=\alpha-\beta\,\ii\] Er zijn nu twee speciale oplossingen: \[\cv{x\\y}=e^{\alpha t}\cv{\cos(\beta t)\\ -\sin(\beta t)}\quad\text{en}\quad e^{\alpha t}\cv{\sin(\beta t)\\ \cos(\beta t)}\] Het superpositiebeginsel van stelsels van lineaire vergelijkingen geeft dat alle oplossingen van de volgende vorm zijn: \[\begin{aligned}\cv{x\\y}&=c_1e^{\alpha t}\cv{\cos(\beta t)\\ -\sin(\beta t)}+c_2e^{\alpha t}\cv{\sin(\beta t)\\ \cos(\beta t)} \\ \\ &=Ae^{\alpha t}\cv{\cos(\beta t+\phi)\\ -\sin(\beta t+\phi)}\end{aligned}\] met constanten \(c_1\), \(c_2\), \(A\) en \(\phi\).
Er zijn 3 gevallen te onderscheiden:
- \(\alpha<0\).
- \(\alpha=0\).
- \(\alpha>0\).
In elk van deze drie gevallen is de stabiliteit van het evenwicht \((0,0)\) anders. We geven steeds een voorbeeld.
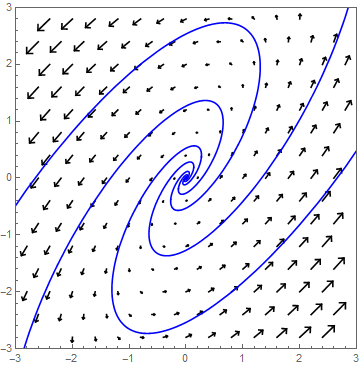
α<0 Stel \(\lambda_{1,2}=\alpha\pm\beta\,\ii\) met \(\alpha<0\). Dan spiraliseren de oplossingen naar de oorsprong. De factor \(e^{\alpha t}\) in de algemene oplossingsformule bepaalt de mate van krimp.
Als voorbeeld bekijken we het stelsel \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{met }A=\matrix{1 & -4\\ 2 & -3}\text.\] De vergelijking voor de eigenwaarden wordt \[\det(A-\lambda I)=(1-\lambda)(-3-\lambda)- (-4)\cdot 2=\lambda^2+2\lambda+5=(\lambda+1)^2+4=0\] De eigenwaarden van \(A\) met bijpassende eigenvectoren zijn dan \[\lambda_1=-1+2\ii \text{ bij }\vec{v}_1=\cv{1+\ii\\1}\quad\text{en}\quad\lambda_2=-1-2\ii\text{ bij }\vec{v}_2=\cv{1-\ii\\1}\text.\] De oplossing is dus \[\cv{x\\y}=c_1e^{-t}\cv{\cos(2t)\\ -\sin(2t)}+c_2e^{-t}\cv{\sin(2t)\\ \cos(2t)}\] waarbij \(c_1\) en \(c_2\) zo gekozen worden dat \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\). In onderstaand faseportret zijn enkele oplossingskrommen getekend.
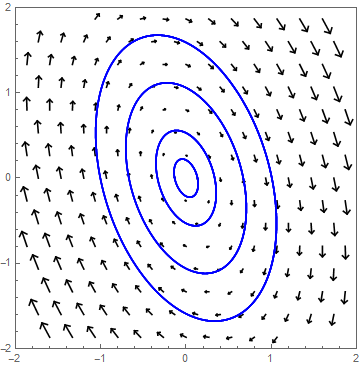
α=0 Stel \(\lambda=\pm\beta\,\ii\) met \(\alpha=0\). Dan zijn de oplossingen periodiek. De banen in het faseportret zijn ellipsen.
Als voorbeeld bekijken we het stelsel \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{met }A=\matrix{1 & 2\\ -5 & -1}\text.\] De vergelijking voor de eigenwaarden wordt \[\det(A-\lambda I)=(1-\lambda)(-1-\lambda)- 2\cdot (-5)=\lambda^2+9=0\] De eigenwaarden van \(A\) met bijpassende eigenvectoren zijn dan \[\lambda_1=3\ii \text{ bij }\vec{v}_1=\cv{-1-3\ii\\5}\quad\text{en}\quad\lambda_2=-3\ii\text{ bij }\vec{v}_2=\cv{-1+3\ii\\5}\text.\] De oplossing is dus \[\cv{x\\y}=c_1\cv{\cos(3t)\\ -\sin(3t)}+c_2\cv{\sin(3t)\\ \cos(3t)}\] waarbij \(c_1\) en \(c_2\) zo gekozen worden dat \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\) In onderstaand faseportret zijn enkele oplossingskrommen getekend.
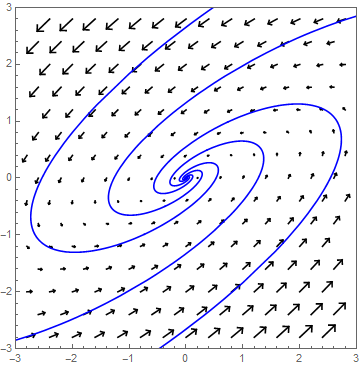
α>0 Stel \(\lambda_{1,2}=\alpha\pm\beta\,\ii\) met \(\alpha>0\). Dan spiraliseren de oplossingen weg van de oorsprong. De factor \(e^{\alpha t}\) in de algemene oplossingsformule bepaalt de mate van groei.
Als voorbeeld bekijken we het stelsel \[\frac{\dd}{\dd t}\cv{x\\ y}=A\cv{x\\ y},\quad \text{met }A=\matrix{3 & -2\\ 4 & -1}\text.\] De vergelijking voor de eigenwaarden wordt \[\det(A-\lambda I)=(3-\lambda)(-1-\lambda)- (-2)\cdot 4=\lambda^2-2\lambda+5=(\lambda-1)^2+4=0\] De eigenwaarden van \(A\) met bijpassende eigenvectoren zijn dan \[\lambda_1=1+2\ii \text{ bij }\vec{v}_1=\cv{1\\1+\ii}\quad\text{en}\quad\lambda_2=1-2\ii\text{ bij }\vec{v}_2=\cv{1\\1-\ii}\text.\] De oplossing is dus \[\cv{x\\y}=c_1e^{t}\cv{\cos(2t)\\ -\sin(2t)}+c_2e^{t}\cv{\sin(2t)\\ \cos(2t)}\] waarbij \(c_1\) en \(c_2\) zo gekozen worden dat \(\cv{x(0)\\ y(0)}=\cv{x_0\\y_0}\). In onderstaand faseportret zijn enkele oplossingskrommen getekend.