Consider a vector quantity \(\vec{x}(t) = \cv{x_1(t)\\ x_2(t)}\) of which the change in time is given by the equation \(\frac{\dd\vec{x}}{\dd t} = A\,\vec{x}\) with matrix \[A =\matrix{0 & 2\\ -2 & 0}\]
-
Calculate the eigenvalues and eigenvectors of \(A\).
-
What is the general formula for the solution \(\vec{x}(t)\) at any time \(t\)?
- What is de equation of the trajectory of the solution for the initial situation \(\vec{x}(0)=\cv{2 \\ 0}\)?
\(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) with \(A = \matrix{0 & 2\\-2 & 0\\}\)
- \(\quad\)The characteristic polynomial of \(A\) is equal to \[\det(A-\lambda\cdot I)=\left|\begin{array}{cc} -\lambda & 2 \\ -2 & -\lambda \end{array}\right|= \lambda^2 +4\]
\(\quad\)The eigenvalues of \(A\) are the zeros of the characteristic polynomial: \(-2\ii\) and \(2\ii\).
\(\quad\)Let \(\cv{v_1\\ v_2}\) be an eigenvector corresponding to the eigenvalue \(2\ii\): \(\matrix{0 & 2\\-2 & 0\\}\cdot \cv{v_1\\ v_2}=2\ii\cv{v_1\\ v_2}\).
\(\quad\)Then: \(\left\{\begin{aligned} 2v_2 &= 2\ii\cdot v_1 \\[0.2cm] -2v_1 &= 2\ii\cdot v_2\end{aligned}\right.\)
\(\quad\)Thus: \(v_2=\ii\cdot v_1\) and \(v_1\) can be freely chosen.
\(\quad\)An eigenvector corresponding to the eigenvalue \(2\ii\) (with integral coefficients) is \(\vec{v}=\cv{1\\\ii}\).
\(\quad\)Similarly, \(\vec{v}=\cv{1\\ -\ii}\) is an eigenvector corresponding to the eigenvalue \(-2\ii\).
- \(\quad\)The general solution is \[\vec{x}(t) =\alpha \cdot\cv{\cos(2t)\\ -\sin(2t)}+ \beta\cdot \cv{\sin(2t)\\ \cos(2t)}\] \(\quad\)with constants \(\alpha\) and \(\beta\).
- \(\quad\vec{x}(0)=\cv{2\\0}\) means that\(x_1(0)=2\) and \(x_2(0)=0\).
\(\quad\)Substitution in the general solution (b) gives: \(\alpha=2\) and \(\beta=2\).
\(\quad\)Thus: \(\vec{x}(t)=2\cv{\cos(2t)\\ -\sin(2t)}\).
\(\quad\)The trajectory is a circle with the origin as centre and radius 2: \[x_1^2+x_2^2=4\] \(\quad\)This is also illustrated in the phase portrait below.
\(\quad\) 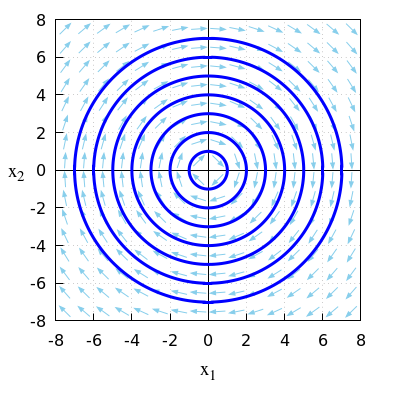
 Pencil-and-paper exercise set 3
Pencil-and-paper exercise set 3




