Systems of differential equations: Linear systems of differential equations
 Classification of stability
Classification of stability
We consider again a pair of coupled homogeneous linear first-order differential equations with constant coefficients of the form \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= a\, x+ b\, y\\[0.25cm] \frac{\dd y}{\dd t} &= c\, x + d\, y\end{aligned}\right.\] and write it in the matrix-vector form \[\frac{\dd}{\dd t}\cv{x\\y}=\matrix{a & b\\ c & d}\cv{x\\y }\] The matrix \[A=\matrix{a & b\\ c & d}\] actually describes the linear system of differential equations. The eigenvalues and eigenvectors determine the nature of the solutions and the stability of the equilibrium \(\cv{x\\y}=\cv{0\\0}\).
The eigenvalues of \(A\) can be written as \[\lambda_{1,2}=\frac{\text{sp}(A)}{2}\pm\frac{1}{2}\sqrt{\bigl(\text{sp}(A)\bigr)^2-4\det(A)}\] where \(\text{sp}(A)=a+d\) is the trace of \(A\) and \(\det(A)=ad-bc\) is the determinant of \(A\).
We have already seen that the equilibrium is attracting when \(A\) has
- two different eigenvalues both of which are negative;
- one negative eigenvalue;
- complex eigenvalues with a real part less than zero.
We can also formulate the stability of the equilibrium in terms of the trace and the determinant of the \(\text{matrix }A\).
For the following system of linear first-order differential equations with constant coefficients in matrix-vector form \[\frac{\dd}{\dd t}\cv{x\\y}=A\cv{x\\y }\quad\text{with}\quad A=\matrix{a & b\\ c & d}\] the following statements are equivalent:
- The equilibrium \((0,0)\) is attracting;
- All eigenvalues of \(A\) have a negative real part;
- \(\det(A)>0\) and \(\text{sp}(A)<0\).
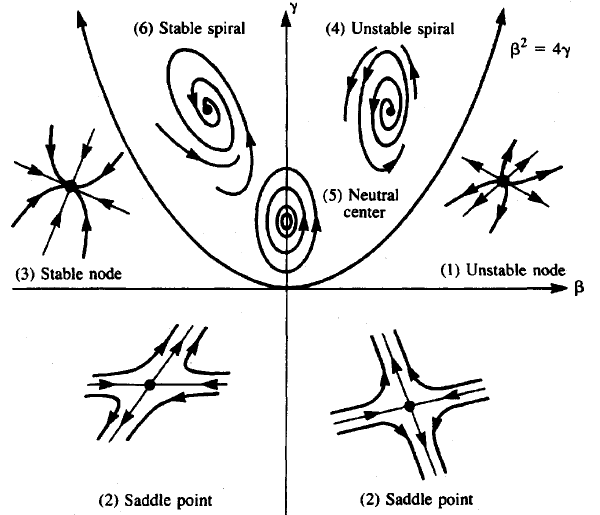
We can explore all combinations of the signs of \(\det(A)\) and \(\text{sp}(A)\) and describe behaviour of solutions near the equilibrium \((0,0)\). The figure below comes from the book Mathematical Models in Biology of Leah Edelstein-Keshet and it summarizes the results. In this figure, \(\beta=\text{sp}(A)\) and \(\gamma=\det(A)\). Then \(\beta^2-4\gamma\) is the discriminant of the characteristic equation of \(A\). When the discriminant is equal to 0, then the stability of the equilibrium depends on the sign of \(\beta\): repelling if \(\beta>0\) and attracting if \(\beta<0\). There are six additional cases:
- repelling equilibrium: \(\beta>0\) and \(\gamma>0\).
- saddle node (semi-stable equilibrium) \(\gamma<0\).
- attracting equilibrium: \(\beta<0\) and \(\gamma>0\).
- expanding spiral: \(\beta>0\) and \(\beta^2<4\gamma\).
- periodic solutions around the equilibrium: \(\beta=0\) and \(\beta^2<4\gamma\).
- shrinking spiral: \(\beta<0\) and \(\beta^2<4\gamma\).