We kijken opnieuw naar een tweetal gekoppelde homogene lineaire eerste-orde differentiaalvergelijkingen met constante coëfficiënten van de vorm \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= a\, x+ b\, y\\[0.25cm] \frac{\dd y}{\dd t} &= c\, x + d\, y\end{aligned}\right.\] en schrijven dit in de matrix-vector vorm \[\frac{\dd}{\dd t}\cv{x\\y}=\matrix{a & b\\ c & d}\cv{x\\y }\] De matrix \[A=\matrix{a & b\\ c & d}\] beschrijft eigenlijk het stelsel van differentiaalvergelijkingen. De eigenwaarden en eigenvectoren bepalen de aard van de oplossingen en de stabiliteit van het evenwicht \(\cv{x\\y}=\cv{0\\0}\).

De eigenwaarden van \(A\) kunnen geschreven worden als \[\lambda_{1,2}=\frac{\text{sp}(A)}{2}\pm\frac{1}{2}\sqrt{\bigl(\text{sp}(A)\bigr)^2-4\det(A)}\] waarbij \(\text{sp}(A)=a+d\) het spoor van \(A\) is en \(\det(A)=ad-bc\) de determinant van \(A\) is.

We hebben al gezien dat het evenwicht aantrekkend is als \(A\)

• twee verschillende eigenwaarden heeft die beiden negatief zijn;
• één negatieve eigenwaarde heeft;
• complexe eigenwaarden heeft met reëel deel kleiner dan nul.

We kunnen de stabiliteit van het evenwicht ook in termen van het spoor en de determinant van de matrix \(A\) formuleren

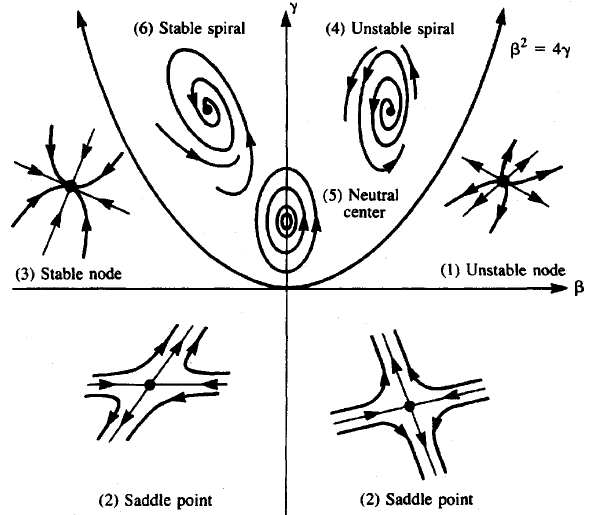
We kunnen alle combinaties van het teken van \(\det(A)\) en \(\text{sp}(A)\) onderzoeken en het gedrag van oplossingen in de buurt van het evenwicht \((0,0)\) beschrijven. Onderstaande figuur afkomstig van het boek Mathematical Models in Biology van Leah Edelstein-Keshet vat de resultaten samen. In deze figuur is \(\beta=\text{sp}(A)\) en \(\gamma=\det(A)\). \(\beta^2-4\gamma\) is de discriminant van de karakteristieke vergelijking van \(A\). Als de discriminant gelijk aan 0 is, dan hangt de stabiliteit van het evenwicht af van het teken van \(\beta\): afstotend als \(\beta>0\) en aantrekkend als \(\beta<0\) . Verder zijn er nog 6 gevallen:

1. afstotend evenwicht: \(\beta>0\) en \(\gamma>0\).
2. zadelpunt (semistabiel evenwicht): \(\gamma<0\).
3. aantrekkend evenwicht: \(\beta<0\) en \(\gamma>0\).
4. uitdijende spiralisering: \(\beta>0\) en \(\beta^2<4\gamma\).
5. periodieke oplossingen rondom het evenwicht: \(\beta=0\) en \(\beta^2<4\gamma\).
6. krimpende spiralisering: \(\beta<0\) en \(\beta^2<4\gamma\).