We consider the system of linear differential equations with the matrix-vector form \[\frac{\dd}{\dd t}\cv{x\\y}=A\cv{x\\y },\quad\text{with}\quad A=\matrix{a & b\\ c & d}\] What type of equilibrium is \((0,0)\) in the following cases, and sketch the phase portrait.
- \(A=\matrix{1 & 1\\ 3 & -1}\)
- \(A=\matrix{2 & 1\\ 2 & 3}\)
- \(A=\matrix{-1 & -2\\ 2 & -1}\)
- \(A=\matrix{1 & 2\\ -2 & 1}\)
- \(A=\matrix{0 & -2\\ 2 & 0}\)
For the linear system of differential equations \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) the nature of the equilibrium \((0,0)\) and the phase portrait depend on the eigenvalues of the matrix \(A\) and their multiplicity.
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) with \(A = \matrix{1 & 1\\3 & -1\\}\)
\(\quad\)The characteristic polynomial of \(A\) is equal to \[\begin{aligned}\det(A-\lambda\, I) &=\left|\begin{array}{cc} 1-\lambda & 1 \\ 3 & -1-\lambda \end{array}\right|\\\\ &= (1-\lambda)(-1-\lambda)-3 \\\\ &=\lambda^2 -4\\\\ &=(\lambda-2)(\lambda+2)\end{aligned}\] \(\quad\)The eigenvalues of \(A\) are the zeros of the characteristic polynomial: \(2\) and \(-2\).
\(\quad\)The equilibrium is a saddle point because there is one positive and one negative eigenvalue.
\(\quad\)Let \(\cv{v_1\\ v_2}\) be an eigenvector corresponding to the eigenvalue \(2\).
\(\quad\)So: \(\matrix{1 & 1\\3 & -1\\}\cdot \cv{v_1\\ v_2}=2\cv{v_1\\ v_2}\).
\(\quad\)Then: \(\left\{\begin{aligned} v_1+v_2 &= 2v_1 \\[0.2cm] 3v_1-v_2 &= 2v_2\end{aligned}\right.\)
\(\quad\)Thus: \(v_2=v_1\) and \(v_1\) can be freely chosen.
\(\quad\)An eigenvector corresponding to the eigenvalue \(2\) (with integral coefficients) is \(\vec{v}=\cv{1\\1}\).
\(\quad\)Similarly, \(\vec{v}=\cv{1\\ -3}\) is an eigenvector corresponding to the eigenvalue \(-2\).
\(\quad\)The general solution is: \[\vec{x}(t)=\alpha e^{2t}\cdot \cv{1\\1}+\beta e^{-2t}\cdot \cv{1\\-3}\] \(\quad\)with constants \(\alpha\) and \(\beta\).
\(\quad\)The figure below shows a phase portrait of this linear system of differential equations.
\(\quad\) 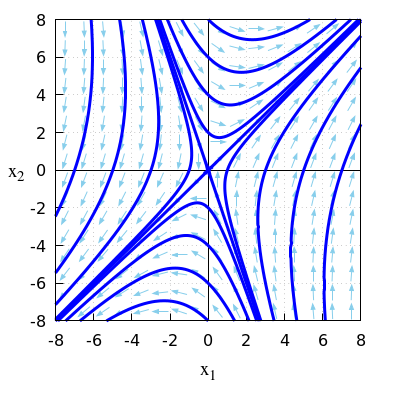
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) with \(A = \matrix{2 & 1\\2 & 3\\}\)
\(\quad\)The characteristic polynomial of \(A\) is equal to \[\begin{aligned}\det(A-\lambda\, I) &=\left|\begin{array}{cc} 2-\lambda & 1 \\ 2 & 3-\lambda \end{array}\right|\\\\ &= (2-\lambda)(3-\lambda)-2 \\\\ &=\lambda^2 -5\lambda+4\\\\ &=(\lambda-1)(\lambda-4)\end{aligned}\] \(\quad\)The eigenvalues of \(A\) are the zeros of the characteristic polynomial: \(1\) and \(4\).
\(\quad\)The equilibrium is repelling because there are two positive eigenvalues.
\(\quad\)Let \(\cv{v_1\\ v_2}\) be an eigenvector with eigenvalue \(1\):
\(\quad\)So: \(\matrix{2 & 1\\2 & 3\\}\cdot \cv{v_1\\ v_2}=\cv{v_1\\ v_2}\).
\(\quad\)Then: \(\left\{\begin{aligned} 2v_1 + V_2 & v_1 = \\[0.2cm] 2v_1+3v_2 &= v_2\end{aligned}\right.\)
\(\quad\)Thus: \(v_2=-v_1\) and \(v_1\) can be freely chosen.
\(\quad\)An eigenvector corresponding to the eigenvalue \(1\) (with integral coefficients) is \(\vec{v}=\cv{1\\-1}\).
\(\quad\)Similarly, \(\vec{v}=\cv{1\\ 2}\) is an eigenvector corresponding to the eigenvalue \(4\).
\(\quad\)The general solution is: \[\vec{x}(t)=\alpha e^{t}\cdot \cv{1\\-1}+\beta e^{4t}\cdot \cv{1\\2}\] \(\quad\)with constants \(\alpha\) and \(\beta\).
\(\quad\)The figure below shows a phase portrait of this linear system of differential equations.
\(\quad\) 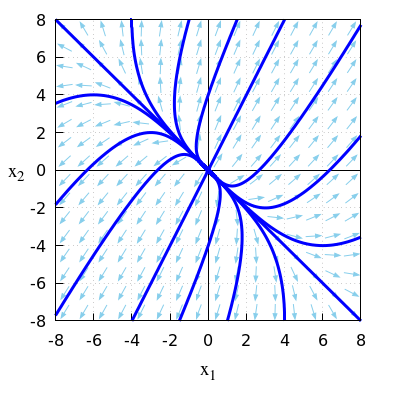
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) with \(A = \matrix{-1 & -2\\2 & -1\\}\)
\(\quad\)The characteristic polynomial of \(A\) is equal to \[\begin{aligned}\det(A-\lambda\, I) &=\left|\begin{array}{cc} -1-\lambda & -2 \\ 2 & -1-\lambda \end{array}\right|\\\\ &= (-1-\lambda)^2+4 \\\\ &= (\lambda+1)^2+4 \\\\&=\lambda^2 +2\lambda+5\end{aligned}\] \(\quad\)The eigenvalues of \(A\) are the zeros of the characteristic polynomial.
\(\quad\)Via the \(abc\)-formula or by completing the square with \((\lambda+1)^2+4\) we get
\(\quad\)the eigenvalues \(-1+2\ii\) and \(-1-2\ii\).
\(\quad\)Complex eigenvalues having a negative real part means
\(\quad\)that we are dealing with a shrinking spiral.
\(\quad\)The figure below shows a phase portrait of this linear system of differential equations.
\(\quad\) 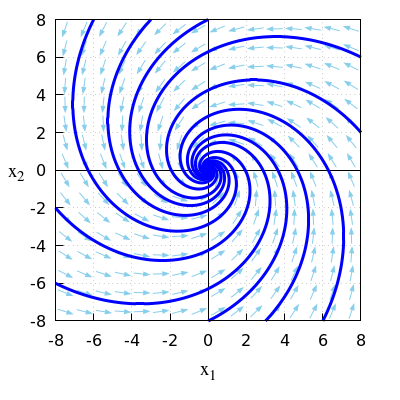
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) with \(A = \matrix{1 & 2\\-2 & 1\\}\)
\(\quad\)The characteristic polynomial of \(A\) is equal to \[\begin{aligned}\det(A-\lambda\, I) &=\left|\begin{array}{cc} 1-\lambda & 2 \\ -2 & 1-\lambda \end{array}\right|\\\\ &= (1-\lambda)^2+4 \\\\ &= (\lambda-1)^2+4 \\\\&=\lambda^2 -2\lambda+5\end{aligned}\] \(\quad\)The eigenvalues of \(A\) are the zeros of the characteristic polynomial.
\(\quad\) Via the \(abc\)-formula or by completing the square with \(\lambda-1)^2+4\) we get
\(\quad\)the eigenvalues \(1+2\ii\) and \(1-2\ii\).
\(\quad\)Complex eigenvalues having a negative real part means
\(\quad\)that we are dealing with an expanding spiral.
\(\quad\)The figure below shows a phase portrait of this linear system of differential equations.
\(\quad\) 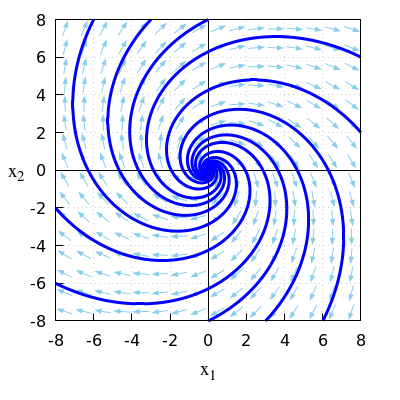
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) with \(A = \matrix{0 & -2\\2 & 0\\}\)
\(\quad\)The characteristic polynomial of \(A\) is equal to \[\begin{aligned}\det(A-\lambda\, I) &=\left|\begin{array}{cc} -\lambda & -2 \\ 2 & \lambda \end{array}\right|\\\\ &= \lambda^2+4 \end{aligned}\] \(\quad\)The eigenvalues of \(A\) are the zeros of the characteristic polynomial.
\(\quad\)Via the \(abc\) -formula or by completing the square with \(\lambda)^2+4\) we get
\(\quad\)the eigenvalues \(2\ii\) and \(-2\ii\) are.
\(\quad\)Complex eigenvalues with a real part equal to \(0\) means
\(\quad\)that we are dealing with circular solution curve.
\(\quad\)The figure below shows a phase portrait in this linear system of differential equations.
\(\quad\)The only differences with the exercise set 3 are the direction of the direction field and the curves.
\(\quad\) 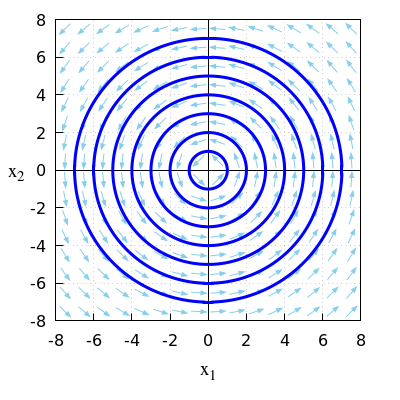
We consider the linear system of differential equations with the matrix-vector form \[\frac{\dd}{\dd t}\cv{x\\y}=A\cv{x\\y },\quad\text{with}\quad A=\matrix{a & b\\ c & d}\] Determine the nature of the stability of \((0,0)\) for the following cases.
- \(A=\matrix{1 & 5\\ 3 & 2}\)
- \(A=\matrix{0 & -2\\ 1 & -3}\)
- \(A=\matrix{-2 & 4\\ -3 & 4}\)
- \(A=\matrix{2 & 1\\ 1 & 3}\)
- \(A=\matrix{-2 & -1\\ 1 & 2}\)
- \(A=\matrix{-1 & -2\\ 2 & 1}\)
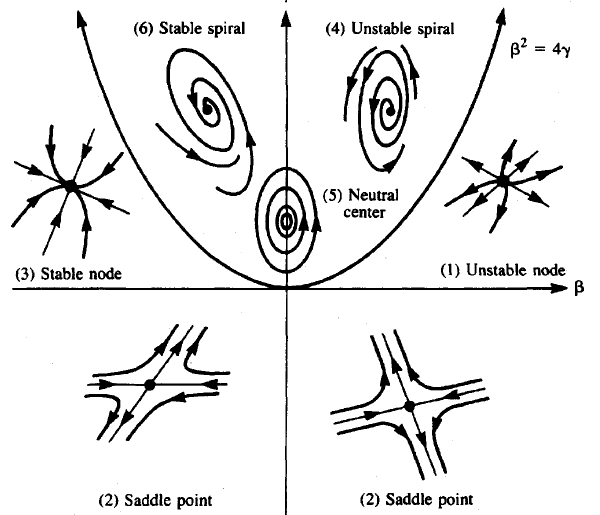
For the linear system \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) the nature of the equilibrium \((0,0)\) depends on the trace and the determinant of the matrix \(A\). We use the scheme below.
In the figure below \(\beta=\mathrm{sp}(A)\) and \(\gamma=\det(A)\). Then \(\beta^2-4\gamma\) is the discriminant of the characteristic equation of \(A\). When the discriminant is equal to 0, then the stability of the balance depends on the sign of \(\beta\): repelling if\(\beta>0\) and attracting if \(\beta<0\). There are six other cases:
- repelling equilibrium: \(\beta>0\) and \(\gamma>0\).
- saddle point (semi-stable equilibrium) \(\gamma<0\).
- attracting equilibrium: \(\beta<0\) and \(\gamma>0\).
- expanding spiral: \(\beta>0\) and \(\beta^2<4\gamma\).
- periodic solutions around the equilibrium: \(\beta=0\) and \(\beta^2<4\gamma\).
- shrinking spiral: \(\beta<0\) and \(\beta^2<4\gamma\).
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) with \(A = \matrix{1 & 5\\3 & 2\\}\)
\(\quad\mathrm{sp}(A)=1+2=3\quad\text{and}\quad\det(A)=1\times 2-5\times 3=-13\).
\(\quad\)Because \(\det(A)<0\) the equilibrium is a saddle point.
\(\quad\)The eigenvalues of matrix \(A\) are \[\lambda_{1,2}=\frac{\mathrm{sp}(A)\pm\sqrt{\mathrm{sp}(A)-4\det(A)}}{2}=\frac{3\pm\sqrt{61}}{2}\] \(\quad\)There is a positive and a negative eigenvalue.
\(\quad\)This confirms that the equilibrium \((0,0)\) is a saddle point.
\(\quad\)The figure below shows a phase portrait in this linear system of differential equations.
\(\quad\) 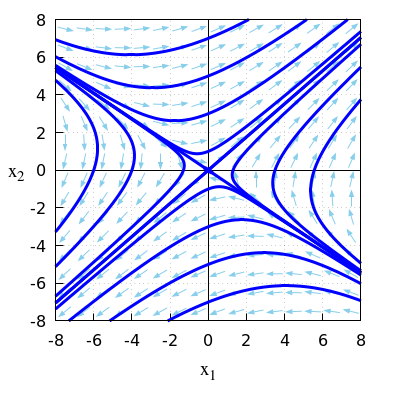
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) with \(A = \matrix{0 & -2\\1 & -3\\}\)
\(\quad\mathrm{sp}(A)=0-3=-3\quad\text{and}\quad\det(A)=0\times (-3)-1\times (-2)=2\).
\(\quad\)Because \(\mathrm{sp}(A)<0\) and \(\det(A)>0\) we have an attracting equilibrium.
\(\quad\)The eigenvalues of the matrix \(A\) are \[\lambda_{1,2}=\frac{\mathrm{sp}(A)\pm\sqrt{\mathrm{sp}(A)-4\det(A)}}{2}=-2\;\;\text{en}\;\; -1\] \(\quad\)Thus, there are two negative eigenvalues.
\(\quad\)This confirms that the equilibrium \((0,0)\) is attracting.
\(\quad\)The figure below shows a phase portrait in this linear system of differential equations.
\(\quad\) 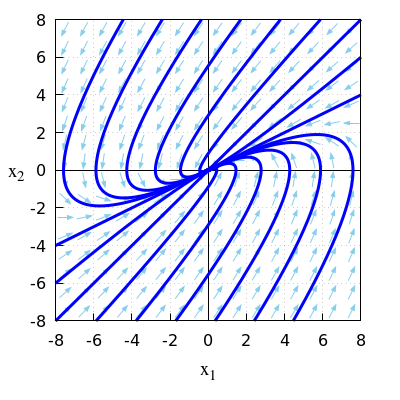
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) with \(A = \matrix{-2 & 4\\-3 & 4\\}\)
\(\quad\mathrm{sp}(A)=-2+4=2\quad\text{and}\quad\det(A)=-2\times 4-4\times (-3)=4\).
\(\quad\)Because \(\mathrm{sp}(A)>0\) and \(\det(A)>0\) we have a repelling equilibrium.
\(\quad\)Because \(\mathrm{sp}(A)>0\) and \(\bigl(\mathrm{sp}(A)\bigr)^2<4\det(A)\) we have an expanding spiral.
\(\quad\)The eigenvalues of the matrix \(A\) are \[\lambda_{1,2}=\frac{\mathrm{sp}(A)\pm\sqrt{\mathrm{sp}(A)-4\det(A)}}{2}=1\pm 3\ii\] \(\quad\)Thus, there are two complex eigenvalues with a positive real part.
\(\quad\)This confirms that the equilibrium \((0,0)\) is repelling
\(\quad\)in the form of an expanding spiral.
\(\quad\)The figure below shows a phase portrait in this linear system of differential equations.
\(\quad\) 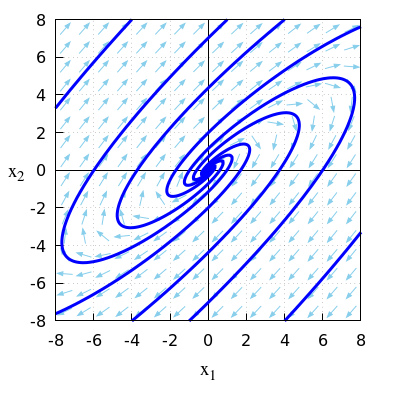
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) with \(A = \matrix{2 & 1\\1 & 3\\}\)
\(\quad\mathrm{sp}(A)=2+3=5\quad\text{and}\quad\det(A)=2\times 3-1\times 1=5\).
\(\quad\)Because \(\mathrm{sp}(A)>0\) and \(\det(A)>0\) we have a repelling equilibrium.
\(\quad\)The eigenvalues of the matrix \(A\) are \[\lambda_{1,2}=\frac{\mathrm{sp}(A)\pm\sqrt{\mathrm{sp}(A)-4\det(A)}}{2}=\frac{5\pm\sqrt{5}}{2}\] \(\quad\)Thus, there are two positive eigenvalues.
\(\quad\)that the equilibrium \((0,0)\) is repelling.
\(\quad\)The figure below shows a phase portrait in this linear system of differential equations.
\(\quad\) 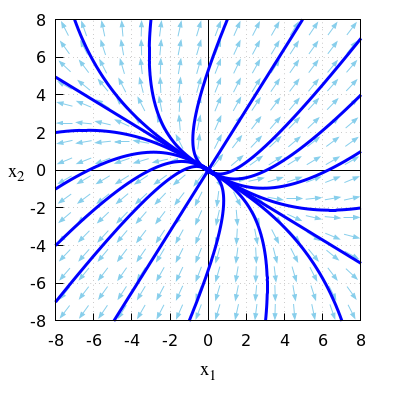
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) with \(A = \matrix{-2 & -1\\1 & 2\\}\)
\(\quad\mathrm{sp}(A)=-2+2=0\quad\text{and}\quad\det(A)=-2\times 2-1\times (-1)=-3\).
\(\quad\)Because \(\det(A)<0\) we have a saddle point.
\(\quad\)The eigenvalues of matrix \(A\) are \[\lambda_{1,2}=\frac{\mathrm{sp}(A)\pm\sqrt{\mathrm{sp}(A)-4\det(A)}}{2}=\pm\sqrt{3}\] \(\quad\)There is a positive and a negative eigenvalue.
\(\quad\)This confirms that the equilibrium \((0,0)\) is a saddle point.
\(\quad\)The figure below shows a phase portrait in this linear system of differential equations.
\(\quad\) 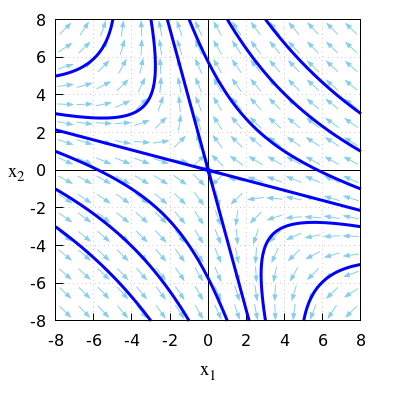
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\, \vec{x}\quad\) with \(A = \matrix{-1 & -2\\2 & 1\\}\)
\(\quad\mathrm{sp}(A)=-1+1=0\quad\text{and}\quad\det(A)=-1\times 1-2\times (-2)=3\).
\(\quad\)Because \(\text{sp(A)=0\) and \(\det(A)>0\) we have periodic solutions around the equilibrium.
\(\quad\)The eigenvalues of the matrix \(A\) are \[\lambda_{1,2}=\frac{\mathrm{sp}(A)\pm\sqrt{\mathrm{sp}(A)-4\det(A)}}{2}=\pm\sqrt{3}\ii\] \(\quad\)Thus, there are two complex eigenvalues with real part equal to \(0\).
\(\quad\)This confirms that we have periodic solutions around the equilibrium \((0,0)\).
\(\quad\)The figure below shows a phase portrait in this linear system of differential equations.
\(\quad\) 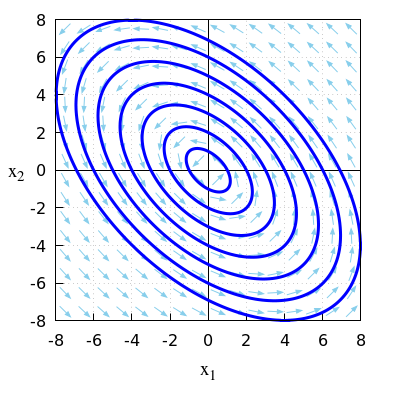
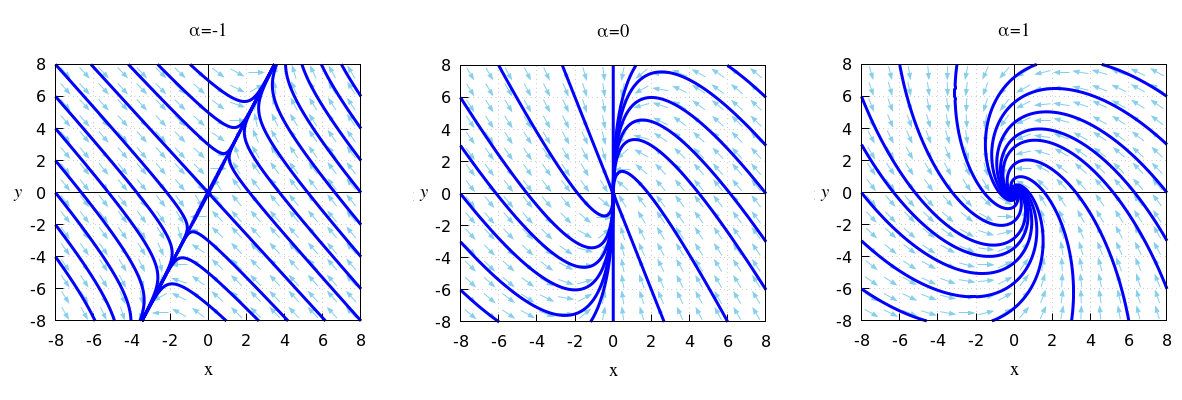
We consider the linear system of differential equations with the matrix-vector form \[\frac{\dd}{\dd t}\cv{x\\y}=A\cv{x\\y },\quad\text{where}\quad A=\matrix{-2 & -\alpha\\ 3 & -1}\] Determine the types of stability of \((0,0)\) that are possible for various values of the parameter \(\alpha\).
We consider the linear system of differential equations with the matrix-vector form \[\frac{\dd}{\dd t}\cv{x\\y}=A\cv{x\\y },\quad\text{where}\quad A=\matrix{-2 & -\alpha\\ 3 & -1}\] Then \[\mathrm{sp}(A)=-1-2=-3\quad\text{and}\quad\det(A)=-(-2)\times (-1)-3\times (-\alpha)=2+3\alpha\] When \(\alpha<-\frac{2}{3}\), then \(\det(A)<0\) and we are dealing with a saddle point.
When \(\alpha>-\frac{2}{3}\) then \(\det(A)>0\) and we are dealing with an attracting equilibrium.
This can be more specific if you look at the expression \(\bigl(\mathrm{sp}(A)\bigr)^2-4\det(A) =9-4(2+3\alpha)=1-12\alpha\). This expression is negative when \(\alpha>\frac{1}{12}\) and this implies according to the stability scheme that we then deal with a shrinking spiral.
When \(-\frac{2}{3}<\alpha\le \frac{1}{12}\) we have a n attracting equilibrium but it is not a shrinking spiral.
The figure below shows phase portraits of this linear system of differential equations for various values of \(\alpha\) that illustrate the three types.
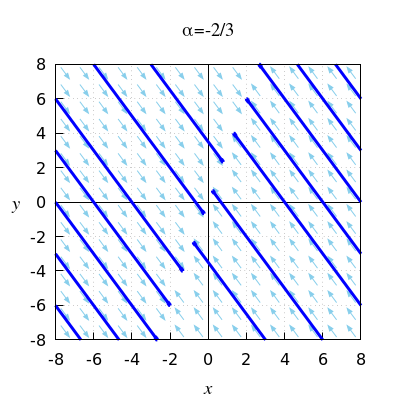
When \(\alpha=-\frac{2}{3}\), we have a special case in which each point on the line \(y=3x\) is an equilibrium. Each solution goes ion a straight line to a point on this line, as in shown in the phase portrait below.
 Pencil-and-paper exercise set 4
Pencil-and-paper exercise set 4
















