We bekijken het stelsel lineaire differentiaalvergelijkingen met de matrix-vector vorm \[\frac{\dd}{\dd t}\cv{x\\y}=A\cv{x\\y },\quad\text{met}\quad A=\matrix{a & b\\ c & d}\] Wat voor type evenwicht is \((0,0)\) voor onderstaande gevallen en schets het faseportret.
- \(A=\matrix{1 & 1\\ 3 & -1}\)
- \(A=\matrix{2 & 1\\ 2 & 3}\)
- \(A=\matrix{-1 & -2\\ 2 & -1}\)
- \(A=\matrix{1 & 2\\ -2 & 1}\)
- \(A=\matrix{0 & -2\\ 2 & 0}\)
Voor het lineaire stelsel \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) hangen de aard van het evenwicht \((0,0)\) en het faseportret af van de eigenwaarden van de matrix \(A\) en hun multipliciteit.
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) met \(A = \matrix{1 & 1\\3 & -1\\}\)
\(\quad\)De karakteristieke veelterm van \(A\) is gelijk aan \[\begin{aligned}\det(A-\lambda\,I) &=\left|\begin{array}{cc} 1-\lambda & 1 \\ 3 & -1-\lambda \end{array}\right|\\\\ &= (1-\lambda)(-1-\lambda)-3 \\\\ &=\lambda^2 -4\\\\ &=(\lambda-2)(\lambda+2)\end{aligned}\]
\(\quad\)De eigenwaarden van \(A\) zijn nulpunten van de karakteristieke veelterm: \(2\) en \(-2\).
\(\quad\)Omdat we één positieve en één negatieve eigenwaarde hebben is het evenwicht een zadelpunt.
\(\quad\)Stel \(\cv{v_1\\ v_2}\) is een eigenvector bij eigenwaarde \(2\): \(\matrix{1 & 1\\3 & -1\\}\cdot \cv{v_1\\ v_2}=2\cv{v_1\\ v_2}\).
\(\quad\)Dan: \(\left\{\begin{aligned} v_1+v_2 &= 2v_1 \\[0.2cm] 3v_1-v_2 &= 2v_2\end{aligned}\right.\)
\(\quad\)Dus: \(v_2=v_1\) en \(v_1\) is dan vrij te kiezen.
\(\quad\)Een eigenvector bij eigenwaarde \(2\) (met gehele coëfficiënten) is \(\vec{v}=\cv{1\\1}\).
\(\quad\)Op net zo'n manier is \(\vec{v}=\cv{1\\ -3}\) een eigenvector bij eigenwaarde \(-2\).
\(\quad\)De algemene oplossing is: \[\vec{x}(t)=\alpha e^{2t}\cdot \cv{1\\1}+\beta e^{-2t}\cdot \cv{1\\-3}\] \(\quad\)met constanten \(\alpha\) en \(\beta\).
\(\quad\)Onderstaande figuur toont een faseportret bij dit lineaire stelsel van differentiaalvergelijkingen.
\(\quad\)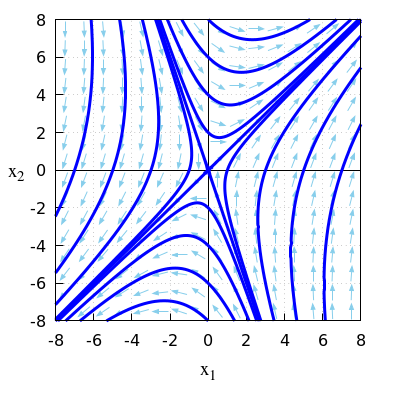
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) met \(A = \matrix{2 & 1\\2 & 3\\}\)
\(\quad\)De karakteristieke veelterm van \(A\) is gelijk aan \[\begin{aligned}\det(A-\lambda\,I) &=\left|\begin{array}{cc} 2-\lambda & 1 \\ 2 & 3-\lambda \end{array}\right|\\\\ &= (2-\lambda)(3-\lambda)-2 \\\\ &=\lambda^2 -5\lambda+4\\\\ &=(\lambda-1)(\lambda-4)\end{aligned}\]
\(\quad\)De eigenwaarden van \(A\) zijn nulpunten van de karakteristieke veelterm: \(1\) en \(4\).
\(\quad\)Omdat we twee positieve eigenwaarden hebben we te maken met een afstotend evenwicht.
\(\quad\)Stel \(\cv{v_1\\ v_2}\) is een eigenvector bij eigenwaarde \(1\): \(\matrix{2 & 1\\2 & 3\\}\cdot \cv{v_1\\ v_2}=\cv{v_1\\ v_2}\).
\(\quad\)Dan: \(\left\{\begin{aligned} 2v_1+v_2 &= v_1 \\[0.2cm] 2v_1+3v_2 &= v_2\end{aligned}\right.\)
\(\quad\)Dus: \(v_2=-v_1\) en \(v_1\) is dan vrij te kiezen.
\(\quad\)Een eigenvector bij eigenwaarde \(1\) (met gehele coëfficiënten) is \(\vec{v}=\cv{1\\-1}\).
\(\quad\)Op net zo'n manier is \(\vec{v}=\cv{1\\ 2}\) een eigenvector bij eigenwaarde \(4\).
\(\quad\)De algemene oplossing is: \[\vec{x}(t)=\alpha e^{t}\cdot \cv{1\\-1}+\beta e^{4t}\cdot \cv{1\\2}\] \(\quad\)met constanten \(\alpha\) en \(\beta\).
\(\quad\)Onderstaande figuur toont een faseportret bij dit lineaire stelsel van differentiaalvergelijkingen.
\(\quad\)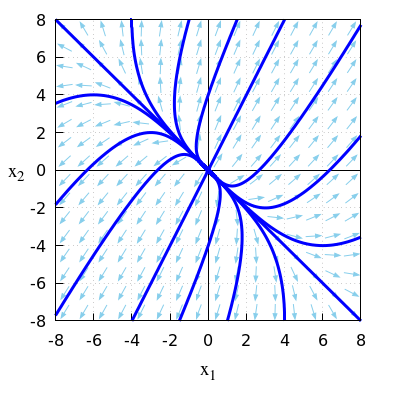
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) met \(A = \matrix{-1 & -2\\2 & -1\\}\)
\(\quad\)De karakteristieke veelterm van \(A\) is gelijk aan \[\begin{aligned}\det(A-\lambda\,I) &=\left|\begin{array}{cc} -1-\lambda & -2 \\ 2 & -1-\lambda \end{array}\right|\\\\ &= (-1-\lambda)^2+4 \\\\ &= (\lambda+1)^2+4 \\\\&=\lambda^2 +2\lambda+5\end{aligned}\]
\(\quad\)De eigenwaarden van \(A\) zijn nulpunten van de karakteristieke veelterm.
\(\quad\)Met de \(abc\)-formule of via kwadraatafsplitsen m.b.v. \((\lambda+1)^2+4\) volgt dat
\(\quad\)de eigenwaarden \(-1+2\ii\) en \(-1-2\ii\) zijn.
\(\quad\)Complexe eigenwaarden met een negatief reëel deel betekent
\(\quad\)dat we te maken hebben met een krimpende spiraal.
\(\quad\)Onderstaande figuur toont een faseportret bij dit lineaire stelsel van differentiaalvergelijkingen.
\(\quad\)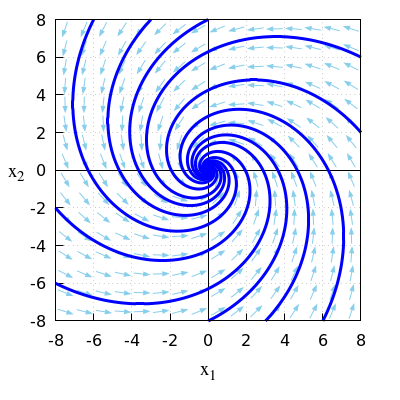
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) met \(A = \matrix{1 & 2\\-2 & 1\\}\)
\(\quad\)De karakteristieke veelterm van \(A\) is gelijk aan \[\begin{aligned}\det(A-\lambda\,I) &=\left|\begin{array}{cc} 1-\lambda & 2 \\ -2 & 1-\lambda \end{array}\right|\\\\ &= (1-\lambda)^2+4 \\\\ &= (\lambda-1)^2+4 \\\\&=\lambda^2 -2\lambda+5\end{aligned}\]
\(\quad\)De eigenwaarden van \(A\) zijn nulpunten van de karakteristieke veelterm.
\(\quad\)Met de \(abc\)-formule of via kwadraatafsplitsen m.b.v. \(\lambda-1)^2+4\) volgt dat
\(\quad\)de eigenwaarden \(1+2\ii\) en \(1-2\ii\) zijn.
\(\quad\)Complexe eigenwaarden met een positief reëel deel betekent
\(\quad\)dat we te maken hebben met een uitdijende spiraal.
\(\quad\)Onderstaande figuur toont een faseportret bij dit lineaire stelsel van differentiaalvergelijkingen.
\(\quad\)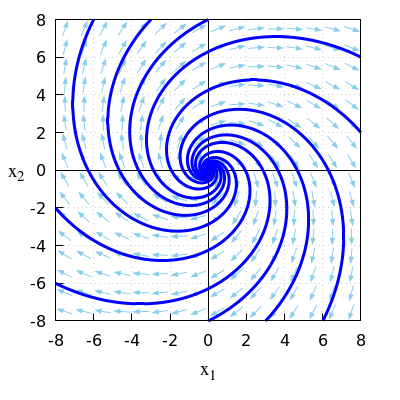
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) met \(A = \matrix{0 & -2\\2 & 0\\}\)
\(\quad\)De karakteristieke veelterm van \(A\) is gelijk aan \[\begin{aligned}\det(A-\lambda\,I) &=\left|\begin{array}{cc} -\lambda & -2 \\ 2 & \lambda \end{array}\right|\\\\ &= \lambda^2+4 \end{aligned}\]
\(\quad\)De eigenwaarden van \(A\) zijn nulpunten van de karakteristieke veelterm.
\(\quad\)Met de \(abc\)-formule of via kwadraatafsplitsen m.b.v. \(\lambda)^2+4\) volgt dat
\(\quad\)de eigenwaarden \(2\ii\) en \(-2\ii\) zijn.
\(\quad\)Complexe eigenwaarden met een reëel deel gelijk aan \(0\) betekent
\(\quad\)dat we te maken hebben met cirkelbanen als oplossingskrommen.
\(\quad\)Onderstaande figuur toont een faseportret bij dit lineaire stelsel van differentiaalvergelijkingen.
\(\quad\)Het enige verschil met Oefeningen 3 is de richting van het richtingsveld en de krommen.
\(\quad\)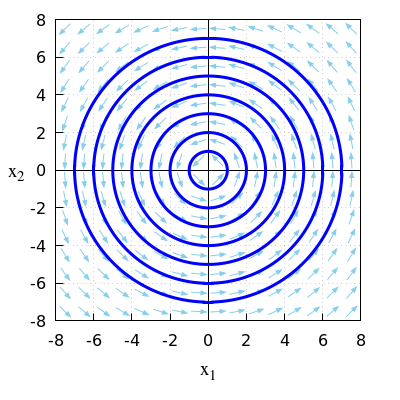
We bekijken het stelsel lineaire differentiaalvergelijkingen met de matrix-vector vorm \[\frac{\dd}{\dd t}\cv{x\\y}=A\cv{x\\y },\quad\text{met}\quad A=\matrix{a & b\\ c & d}\] Bepaal de aard van de stabiliteit van \((0,0)\) voor onderstaande gevallen.
- \(A=\matrix{1 & 5\\ 3 & 2}\)
- \(A=\matrix{0 & -2\\ 1 & -3}\)
- \(A=\matrix{-2 & 4\\ -3 & 4}\)
- \(A=\matrix{2 & 1\\ 1 & 3}\)
- \(A=\matrix{-2 & -1\\ 1 & 2}\)
- \(A=\matrix{-1 & -2\\ 2 & 1}\)
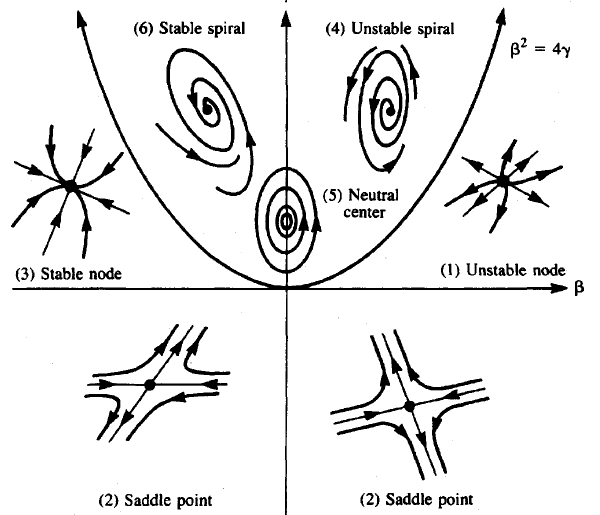
Voor het lineaire stelsel \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) hangt de aard van het evenwicht \((0,0)\) af van het spoor en de determinant van de matrix \(A\). We gebruiken hiervoor het onderstaande schema.
In onderstaande figuur is \(\beta=\mathrm{sp}(A)\) en \(\gamma=\det(A)\). Dan is \(\beta^2-4\gamma\) de discriminant van de karakteristieke vergelijking van \(A\). Als de discriminant gelijk aan 0 is, dan hangt de stabiliteit van het evenwicht af van het teken van \(\beta\): afstotend als \(\beta>0\) en aantrekkend als \(\beta<0\) . Verder zijn er nog 6 gevallen:
- afstotend evenwicht: \(\beta>0\) en \(\gamma>0\).
- zadelpunt (semistabiel evenwicht): \(\gamma<0\).
- aantrekkend evenwicht: \(\beta<0\) en \(\gamma>0\).
- uitdijende spiralisering: \(\beta>0\) en \(\beta^2<4\gamma\).
- periodieke oplossingen rondom het evenwicht: \(\beta=0\) en \(\beta^2<4\gamma\).
- krimpende spiralisering: \(\beta<0\) en \(\beta^2<4\gamma\).
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) met \(A = \matrix{1 & 5\\3 & 2\\}\)
\(\quad\mathrm{sp}(A)=1+2=3\quad\text{en}\quad\det(A)=1\times 2-5\times 3=-13\).
\(\quad\)Omdat \(\det(A)<0\) is het evenwicht een zadelpunt.
\(\quad\)De eigenwaarden van de matrix \(A\) zijn \[\lambda_{1,2}=\frac{\mathrm{sp}(A)\pm\sqrt{\mathrm{sp}(A)-4\det(A)}}{2}=\frac{3\pm\sqrt{61}}{2}\] \(\quad\)Er is dus één positieve en een negatieve eigenwaarde.
\(\quad\)Dit bevestigt dat het evenwicht \((0,0)\) een zadelpunt is.
\(\quad\)Onderstaand faseportret bij dit lineaire stelsel van differentiaalvergelijkingen bevestigt het ook.
\(\quad\)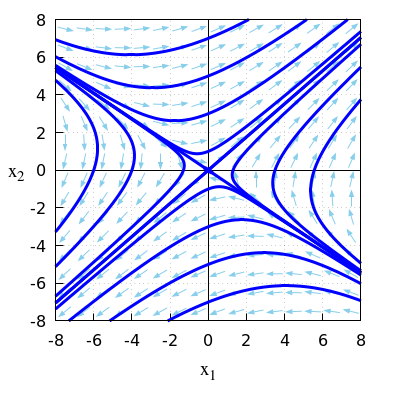
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) met \(A = \matrix{0 & -2\\1 & -3\\}\)
\(\quad\mathrm{sp}(A)=0-3=-3\quad\text{en}\quad\det(A)=0\times (-3)-1\times (-2)=2\).
\(\quad\)Omdat \(\mathrm{sp}(A)<0\) en \(\det(A)>0\) is het evenwicht aantrekkend.
\(\quad\)De eigenwaarden van de matrix \(A\) zijn \[\lambda_{1,2}=\frac{\mathrm{sp}(A)\pm\sqrt{\mathrm{sp}(A)-4\det(A)}}{2}=-2\;\;\text{en}\;\; -1\] \(\quad\)Er zijn dus twee negatieve eigenwaarden.
\(\quad\)Dit bevestigt dat het evenwicht \((0,0)\) aantrekkend is.
\(\quad\)Onderstaand faseportret bij dit lineaire stelsel van differentiaalvergelijkingen bevestigt het ook.
\(\quad\)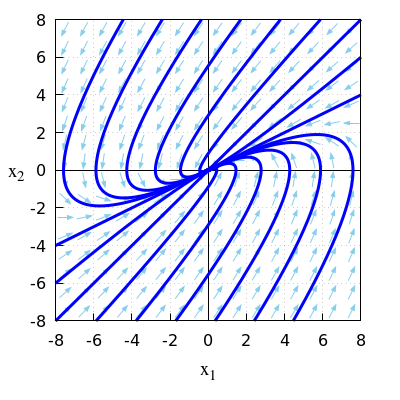
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) met \(A = \matrix{-2 & 4\\-3 & 4\\}\)
\(\quad\mathrm{sp}(A)=-2+4=2\quad\text{en}\quad\det(A)=-2\times 4-4\times (-3)=4\).
\(\quad\)Omdat \(\mathrm{sp}(A)>0\) en \(\det(A)>0\) is het evenwicht afstotend.
\(\quad\)Omdat \(\mathrm{sp}(A)>0\) en \(\bigl(\mathrm{sp}(A)\bigr)^2<4\det(A)\) is er sprake van een uitdijende spiralisering.
\(\quad\)De eigenwaarden van de matrix \(A\) zijn \[\lambda_{1,2}=\frac{\mathrm{sp}(A)\pm\sqrt{\mathrm{sp}(A)-4\det(A)}}{2}=1\pm 3\ii\] \(\quad\)Er zijn dus twee complexe eigenwaarden met positief reëel deel.
\(\quad\)Dit bevestigt dat het evenwicht \((0,0)\) afstotend is met uitdijende spiralisering.
\(\quad\)Onderstaand faseportret bij dit lineaire stelsel van differentiaalvergelijkingen bevestigt het ook.
\(\quad\)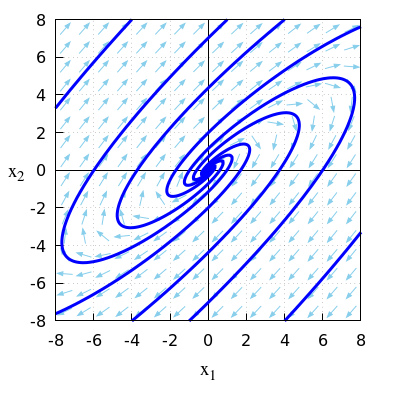
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) met \(A = \matrix{2 & 1\\1 & 3\\}\)
\(\quad\mathrm{sp}(A)=2+3=5\quad\text{en}\quad\det(A)=2\times 3-1\times 1=5\).
\(\quad\)Omdat \(\mathrm{sp}(A)>0\) en \(\det(A)>0\) is het evenwicht afstotend.
\(\quad\)De eigenwaarden van de matrix \(A\) zijn \[\lambda_{1,2}=\frac{\mathrm{sp}(A)\pm\sqrt{\mathrm{sp}(A)-4\det(A)}}{2}=\frac{5\pm\sqrt{5}}{2}\] \(\quad\)Er zijn dus twee positieve eigenwaarden.
\(\quad\)Dit bevestigt dat het evenwicht \((0,0)\) afstotend is.
\(\quad\)Onderstaand faseportret bij dit lineaire stelsel van differentiaalvergelijkingen bevestigt het ook.
\(\quad\)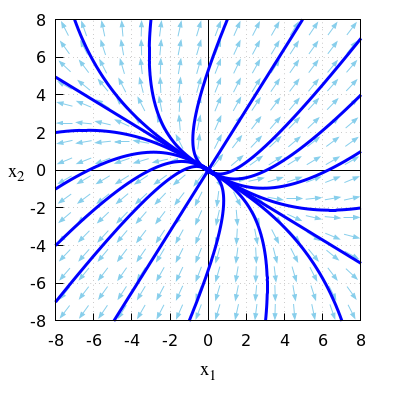
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) met \(A = \matrix{-2 & -1\\1 & 2\\}\)
\(\quad\mathrm{sp}(A)=-2+2=0\quad\text{en}\quad\det(A)=-2\times 2-1\times (-1)=-3\).
\(\quad\)Omdat \(\det(A)<0\) is het evenwicht een zadelpunt.
\(\quad\)De eigenwaarden van de matrix \(A\) zijn \[\lambda_{1,2}=\frac{\mathrm{sp}(A)\pm\sqrt{\mathrm{sp}(A)-4\det(A)}}{2}=\pm\sqrt{3}\] \(\quad\)Er is dus één positieve en een negatieve eigenwaarde.
\(\quad\)Dit bevestigt dat het evenwicht \((0,0)\) een zadelpunt is.
\(\quad\)Onderstaand faseportret bij dit lineaire stelsel van differentiaalvergelijkingen bevestigt het ook.
\(\quad\)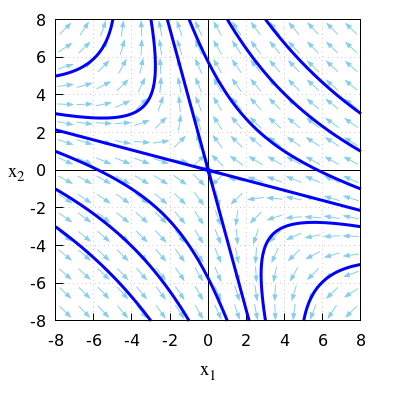
- \(\quad\frac{\dd}{\dd t}\vec{x}=A\,\vec{x}\quad\) met \(A = \matrix{-1 & -2\\2 & 1\\}\)
\(\quad\mathrm{sp}(A)=-1+1=0\quad\text{en}\quad\det(A)=-1\times 1-2\times (-2)=3\).
\(\quad\)Omdat \(\mathrm{sp}(A)=0\) en \(\det(A)>0\) hebben we periodieke oplossingen rondom het evenwicht.
\(\quad\)De eigenwaarden van de matrix \(A\) zijn \[\lambda_{1,2}=\frac{\mathrm{sp}(A)\pm\sqrt{\mathrm{sp}(A)-4\det(A)}}{2}=\pm\sqrt{3}\ii\] \(\quad\)Er zijn de complexe eigenwaarden met reëel deel gelijk aan \(0\).
\(\quad\)Dit bevestigt periodieke oplossingen rondom het evenwicht \((0,0)\).
\(\quad\)Onderstaand faseportret bij dit lineaire stelsel van differentiaalvergelijkingen bevestigt het ook.
\(\quad\)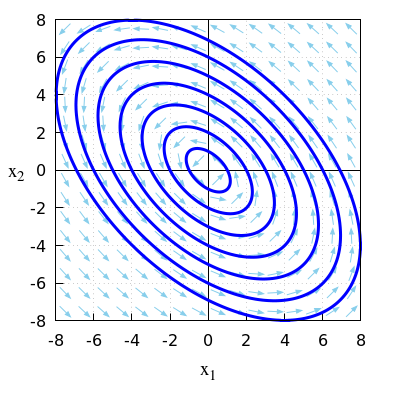
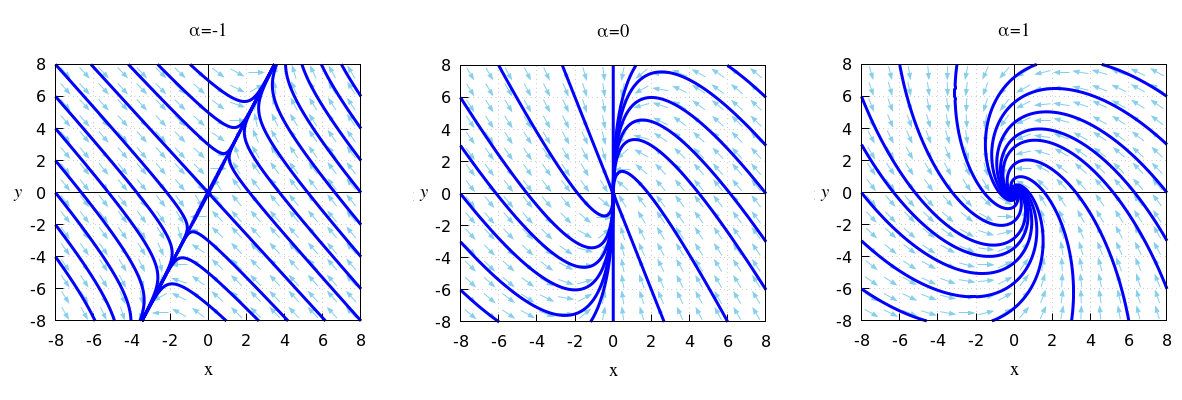
We bekijken het stelsel lineaire differentiaalvergelijkingen met de matrix-vector vorm \[\frac{\dd}{\dd t}\cv{x\\y}=A\cv{x\\y },\quad\text{met}\quad A=\matrix{-2 & -\alpha\\ 3 & -1}\] Bepaal de typen van stabiliteit van \((0,0)\) die mogelijk zijn voor verschillende waarden van de parameter \(\alpha\).
We bekijken het stelsel lineaire differentiaalvergelijkingen met de matrix-vector vorm \[\frac{\dd}{\dd t}\cv{x\\y}=A\cv{x\\y },\quad\text{met}\quad A=\matrix{-2 & -\alpha\\ 3 & -1}\] Dan \[\mathrm{sp}(A)=-1-2=-3\quad\text{en}\quad\det(A)=-(-2)\times (-1)-3\times (-\alpha)=2+3\alpha\] Als \(\alpha<-\frac{2}{3}\), dan \(\det(A)<0\) en hebben we te maken met een zadelpunt.
Als \(\alpha>-\frac{2}{3}\), dan \(\det(A)>0\) en hebben we te maken met een aantrekkend evenwicht.
Dit kan nog specifieker als je kijkt naar de uitdrukking \(\bigl(\mathrm{sp}(A)\bigr)^2-4\det(A) =9-4(2+3\alpha)=1-12\alpha\). Deze uitdrukking is negatief als \(\alpha>\frac{1}{12}\) en dit impliceert volgens het stabiliteitsschema dat we dan te maken hebben met krimpende spiralisering.
Als \(-\frac{2}{3}<\alpha\le \frac{1}{12}\) dan hebben we een aantrekkend evenwicht zonder krimpende spiralisering.
Onderstaande figuur toont faseportretten bij dit lineaire stelsel van differentiaalvergelijkingen voor verschillende waarden van \(\alpha\) die de drie types illustreren.
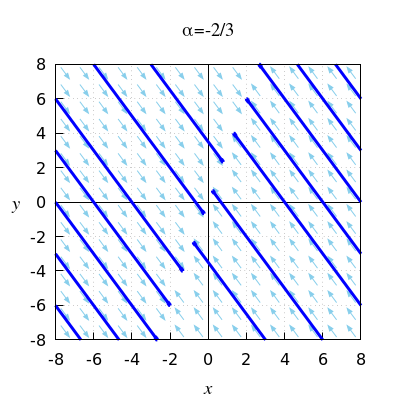
Als \(\alpha=-\frac{2}{3}\), dan hebben we een speciaal geval waarin elk punt op de lijn \(y=3x\) een evenwicht is. Elke oplossing gaat in een rechte lijn naar een punt op deze lijn zoals in onderstaand faseportret te zien is.
 Pen-en-papier oefeningen 4
Pen-en-papier oefeningen 4
















