Pencil-and-paper exercise set 5

Systems of differential equations: Linear systems of differential equations

Pencil-and-paper exercise set 5

Stability scheme \(\beta=\mathrm{sp}=a+d\) and \(\gamma=\det=ad-bc\) for the system \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= a\, x+ b\, y\\[0.25cm] \frac{\dd y}{\dd t} &= c\, x + d\, y\end{aligned}\right.\]

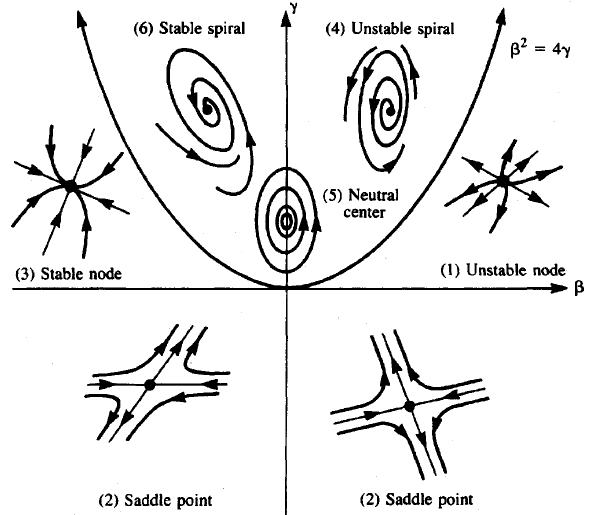
Assignment 1 Use the above stability scheme to determine the nature of the equilibrium \((0,0)\) of the below system of differential equations: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -4x+ 2y\\ \\ \frac{\dd y}{\dd t} &= x -2y\end{aligned}\right.\]

Worked-out solution In this case: \[a=-4,\quad b=2,\quad c=1,\quad d=-2\] Then \[\beta\,(=a+d)=-6,\quad \gamma\,(=ad-bc)=6\] Because \(\beta<0\), \(\gamma>0\) and \(\beta^2-4\gamma=12>0\), there is, according to the stability scheme, an attracting equilibrium \((0,0)\) with solution curves that approach it, but not in a spiral shape.

Assignment 2 Use the above stability scheme to determine the nature of the equilibrium \((0,0)\) of the below system of differential equations: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= x-y\\ \\ \frac{\dd y}{\dd t} &= x-2y\end{aligned}\right.\]

Worked-out solution In this case: \[a=1,\quad b=-1,\quad c=1,\quad d=-2\] Then \[\beta\,(=a+d)=-1,\quad \gamma\,(=ad-bc)=-1\] Because \(\beta<0\) and \(\gamma<0\) there is, according to the stability scheme, a saddle point in \((0,0)\).

Assignment 3 Use the above stability scheme to determine the nature of the equilibrium \((0,0)\) of the below system of differential equations: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= x-y\\ \\ \frac{\dd y}{\dd t} &= 2x-y\end{aligned}\right.\]

Worked-out solution In this case: \[a=1,\quad b=-1,\quad c=2,\quad d=-1\] Then \[\beta\,(=a+d)=0,\quad \gamma\,(=ad-bc)=1\] Because \(\beta=0\) and \(\gamma>0\) there is, according to the stability scheme, an equilibrium \((0,0)\) around which the solution curves move around in elliptical orbits.

Assignment 4 Use the above stability scheme to determine the nature of the equilibrium \((0,0)\) of the below system of differential equations: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= x-y\\ \\ \frac{\dd y}{\dd t} &= 2x+y\end{aligned}\right.\]

Worked-out solution In this case: \[a=1,\quad b=-1,\quad c=2,\quad d=1\] Then \[\beta\,(=a+d)=2,\quad \gamma\,(=ad-bc)=3\] Because \(\beta<0\), \(\gamma>0\) and \(\beta^2-4\gamma=-5<0\) there is, according to the stability scheme, a repelling equilibrium \((0,0)\) with solution curves that move away from it in spiral form.

Assignment 5 Use the above stability scheme to determine the nature of the equilibrium \((0,0)\) of the below system of differential equations: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -x-y\\ \\ \frac{\dd y}{\dd t} &= 2x-y\end{aligned}\right.\]

Worked-out solution In this case \[a=-1,\quad b=-1,\quad c=2,\quad d=-1\] Then \[\beta\,(=a+d)=-2,\quad \gamma\,(=ad-bc)=3\] Because \(\beta<0\), \(\gamma>0\) and \(\beta^2-4\gamma=-8<0\) there is, according to the stability diagram, an attracting equilibrium \((0,0)\) with solution curves that approach it in a spiral form.