Pen-en-papier opdracht: stabiliteitsanalyse

Stelsels van differentiaalvergelijkingen: Lineaire stelsels van differentiaalvergelijkingen

Pen-en-papier opdracht: stabiliteitsanalyse

Stabiliteitsschema \(\beta=\mathrm{sp}=a+d\) en \(\gamma=\det=ad-bc\) voor het stelsel \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= a\, x+ b\, y\\ \frac{\dd y}{\dd t} &= c\, x + d\, y\end{aligned}\right.\]

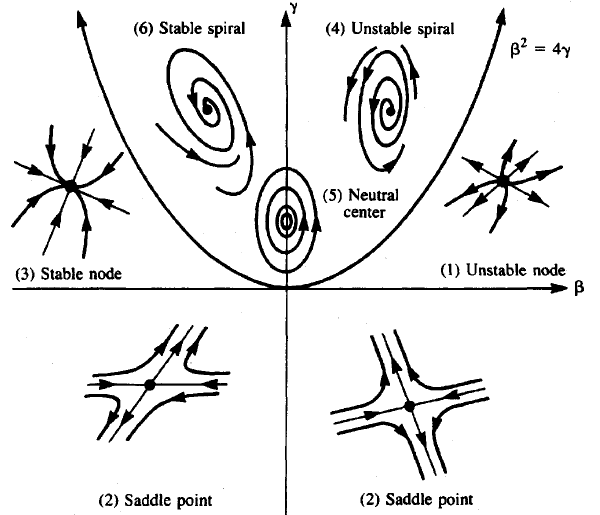
Opdracht 1 Gebruik het bovenstaande stabiliteitsschema om de aard van het evenwicht \((0,0)\) te bepalen van onderstaand stelsel van differentiaalvergelijkingen: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -4x+ 2y\\ \\ \frac{\dd y}{\dd t} &= x -2y\end{aligned}\right.\]

Uitwerking In dit geval: \[a=-4,\quad b=2,\quad c=1,\quad d=-2\] Dan \[\beta\,(=a+d)=-6,\quad \gamma\,(=ad-bc)=6\] Omdat \(\beta<0\), \(\gamma>0\) en \(\beta^2-4\gamma=12>0\) is er volgens het stabiliteitsschema sprake van een aantrekkend evenwicht \((0,0)\) met oplossingskrommen die daarheen lopen, maar niet in spiraalvorm.

Opdracht 2 Gebruik het bovenstaande stabiliteitsschema om de aard van het evenwicht \((0,0)\) te bepalen van onderstaand stelsel van differentiaalvergelijkingen: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= x-y\\ \\ \frac{\dd y}{\dd t} &= x-2y\end{aligned}\right.\]

Uitwerking In dit geval: \[a=1,\quad b=-1,\quad c=1,\quad d=-2\] Dan \[\beta\,(=a+d)=-1,\quad \gamma\,(=ad-bc)=-1\] Omdat \(\beta<0\) en \(\gamma<0\) is er volgens het stabiliteitsschema sprake van een zadelpunt \((0,0)\).

Opdracht 3 Gebruik het bovenstaande stabiliteitsschema om de aard van het evenwicht \((0,0)\) te bepalen van onderstaand stelsel van differentiaalvergelijkingen: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= x-y\\ \\ \frac{\dd y}{\dd t} &= 2x-y\end{aligned}\right.\]

Uitwerking In dit geval: \[a=1,\quad b=-1,\quad c=2,\quad d=-1\] Dan \[\beta\,(=a+d)=0,\quad \gamma\,(=ad-bc)=1\] Omdat \(\beta=0\) en \(\gamma>0\) is er volgens het stabiliteitsschema sprake van een evenwicht \((0,0)\) waar omheen de oplossingskrommen in ellipsbanen cirkelen.

Opdracht 4 Gebruik het bovenstaande stabiliteitsschema om de aard van het evenwicht \((0,0)\) te bepalen van onderstaand stelsel van differentiaalvergelijkingen: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= x-y\\ \\ \frac{\dd y}{\dd t} &= 2x+y\end{aligned}\right.\]

Uitwerking In dit geval: \[a=1,\quad b=-1,\quad c=2,\quad d=1\] Dan \[\beta\,(=a+d)=2,\quad \gamma\,(=ad-bc)=3\] Omdat \(\beta<0\), \(\gamma>0\) en \(\beta^2-4\gamma=-5<0\) is er volgens het stabiliteitsschema sprake van een afstotend evenwicht \((0,0)\) met oplossingskrommen die daar in spiraalvorm vandaan lopen.

Opdracht 5 Gebruik het bovenstaande stabiliteitsschema om de aard van het evenwicht \((0,0)\) te bepalen van onderstaand stelsel van differentiaalvergelijkingen: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -x-y\\ \\ \frac{\dd y}{\dd t} &= 2x-y\end{aligned}\right.\]

Uitwerking In dit geval: \[a=-1,\quad b=-1,\quad c=2,\quad d=-1\] Dan \[\beta\,(=a+d)=-2,\quad \gamma\,(=ad-bc)=3\] Omdat \(\beta<0\), \(\gamma>0\) en \(\beta^2-4\gamma=-8<0\) is er volgens het stabiliteitsschema sprake van een aantrekkend evenwicht \((0,0)\) met oplossingskrommen die daar in spiraalvorm naartoe lopen.