Stelsels van differentiaalvergelijkingen: Niet-lineaire differentiaalvergelijkingen
 Het fasevlak
Het fasevlak
Voor stelsels van lineaire eerste-orde differentiaalvergelijkingen hebben we begrippen als fasevlak, faseportret, richtingsveld, isoclienen en evenwicht geïntroduceerd. Deze kunnen ook voor niet-lineaire stelsels van eerste-orde differentiaalvergelijkingen gebruikt worden, bijvoorbeeld voor stelsels van differentiaalvergelijkingen van de vorm \[\left\{\begin{aligned} \dfrac{\dd x}{\dd t} &= f(x,y)\\[0.25cm] \dfrac{\dd y}{\dd t} &= g(x,y)\end{aligned}\right.\] op het vlak, waarbij \(f\) en \(g\) "nette" functie zijn ("net" betekent hier dat afgeleiden bestaan en continue functies zijn).
Beginwaardeprobleem Bij een gegeven keuze van \((x_0,y_0)\in \mathbb{R}^2\) bestaat er precies één kromme \(t\mapsto \bigl(x(t),y(t)\bigr)\) die aan het voorgaande stelsel voldoet en waarvoor \(\bigl(x(0),y(0)\bigr)=(x_0,y_0)\).
Evenwicht Als \(f(x_0,y_0)=g(x_0,y_0)=0\) dan heet \((x_0,y_0)\) een singulier punt en ook wel een evenwicht en dan is deze kromme constant: \(\bigl(x(t),y(t)\bigr)=(x_0,y_0)\) voor alle \(t\). Als \((x_0,y_0)\) niet een singulier punt is dan is deze functie \(t\mapsto \bigl(x(t),y(t)\bigr)\) niet constant (d.w.z. echt een kromme i.p.v. een punt) en deze kromme noemt men de oplossingskromme door \((x_0,y_0)\).
Faseportret Vaak tekent men een aantal oplossingskrommen in één figuur, en zoiets wordt dan een faseportret genoemd. Tevens wordt dan geregeld het vectorveld horende bij het 2-dimensionale stelsel differentiaalvergelijkingen getekend. Bij elk punt \((x,y)\) in het faseportret kunnen we namelijk de vector \(\cv{x'\\y'}\) berekenen als \(\cv{f(x,y)\\g(x,y)}\) en tekenen in het vlak. Vaak gaat hierbij de aandacht uit naar de verzameling punten in het vlak waarin de vector \(\cv{x'\\y'}\) constant is, de zogenaamde isoclienen. Speciaal wordt gekeken naar \(\boldsymbol{x}\)-nul-isoclienen en \(\boldsymbol{y}\)-nul-isoclienen, dat wil zeggen, naar punten waarvoor \(\frac{\dd x}{\dd t}=0\) respectievelijk \(\frac{\dd y}{\dd t}=0\). Singuliere punten zijn dan snijpunten van \(x\)-nul-isoclienen en \(y\)-nul-isoclienen.
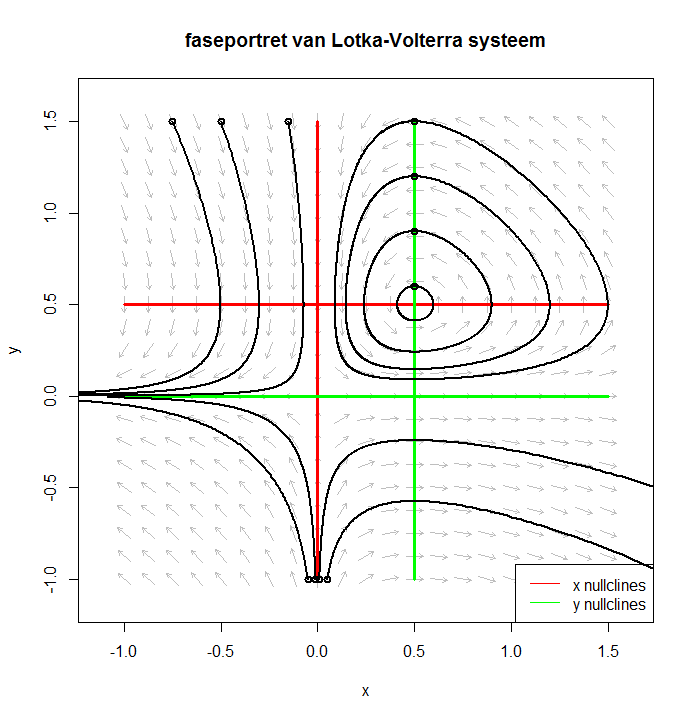
Lotka-Volterra vergelijking We bekijken een Lotka-Volterra systeem, dat bijvoorbeeld gebruikt wordt bij roofdier-prooidier modellen: \[\left\{\begin{aligned} \dfrac{\dd x}{\dd t} & =a x-b x y\\[0.25cm] \dfrac{\dd y}{\dd t} & =-c y+d x y\end{aligned}\right.\] Als voorbeeld nemen we \(a=c=1\) en \(b=d=2\). Onderstaand faseplaatje illustreert dat er nu verschillende typen oplossingskrommen zijn: de periodieke banen in het eerste kwadrant springen in het oog. De periodieke banen lopen rond het evenwicht \((\tfrac{1}{2},\tfrac{1}{2})\). Als je in zo'n periodieke baan zit en er treedt een verstoring op, dan ga je naar een periodieke baan met een andere 'amplitude'. Het evenwicht \((0,0)\) is een zadelpunt. Wanneer \(x\) en \(y\) grootheden zijn die alleen niet-negatieve waarden kunnen aannemen, dan is dit zadelpunt niet zo interessant. De rode lijnen vormen de \(x\)-nul-isoclienen, d.w.z. de punten waarin de richting van oplossingskrommen verticaal is, en de groene lijnen vormen de \(y\)-nul-isoclienen, d.w.z. de punten waarin de richting van oplossingskrommen horizontaal is.
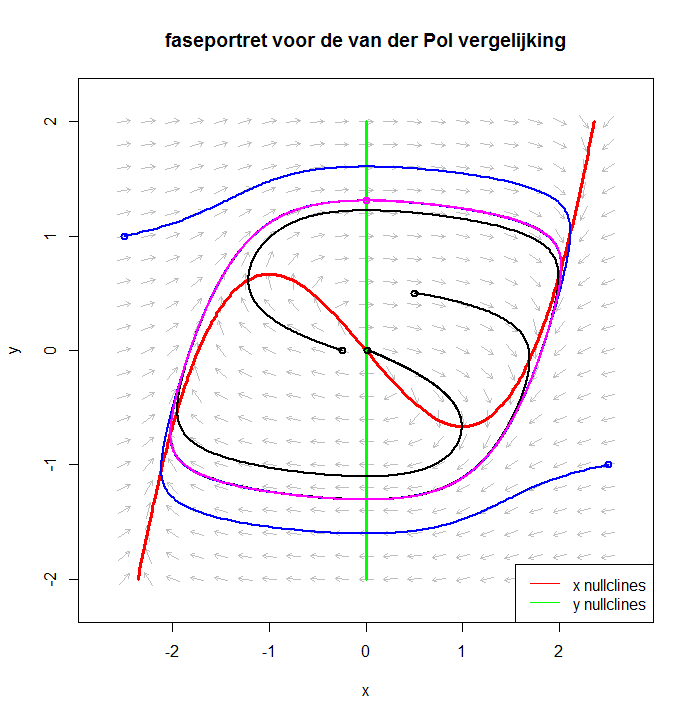
Van der Pol vergelijking We bekijken de Van der Pol vergelijking \[\left\{\begin{aligned} \dfrac{\dd x}{\dd t} & =\frac{1}{\varepsilon}\left(y+x-\frac{x^3}{3}\right)\\[0.25cm] \dfrac{\dd y}{\dd t} & =-\varepsilon x\end{aligned}\right.\] met \(0<\varepsilon\ll 1\). Als voorbeeld nemen we een tamelijk grote waarde \(\varepsilon=\tfrac{1}{2}\) om duidelijker te kunnen laten zien wat er gebeurt. Onderstaand faseplaatje illustreert dat er nu een ander type oplossing bestaat: de limietcyclus. Dit is een periodieke baan, hier in de kleur magenta getekend, waarnaar oplossingen convergeren. We hebben in onderstaande figuur twee soorten oplossingskrommen getekend: drie krommen die van binnenin naar de limiet cyclus convergeert (zwarte krommen), en twee krommen die van buitenuit naar de limiet cyclus convergeert (blauwe krommen). Een kleine verstoring van het systeem maakt niet zo veel uit want je convergeert daarna kennelijk toch weer naar de limiet cyclus. De rode lijnen vormen de \(x\)-nul-isoclienen, d.w.z. de punten waarin de richting van oplossingskrommen verticaal is, en de groene lijnen vormen de \(y\)-nul-isoclienen, d.w.z. de punten waarin de richting van oplossingskrommen horizontaal is.
Interactieve computerversie van een faseportret Je kunt ter inspiratie ook spelen met onderstaande interactieve computerversie van een faseportret van een niet-lineair stelsel van differentiaalvergelijkingen met een parameter \(a\).
In deze sectie gaan we opnieuw kijken naar het gedrag van oplossingen in de buurt van een evenwicht.


