We bekijken het stelsel differentiaalvergelijkingen \[\left\{\begin{aligned} \dfrac{\dd x}{\dd t} &= -x+x^3\\[0.25cm] \dfrac{\dd y}{\dd t} &= -2y \end{aligned}\right.\] Evenwichten zijn er als \(\dfrac{\dd x}{\dd t}=0\) en \(\dfrac{\dd y}{\dd t}=0\), dus als \(-x+x^3=x(x-1)(x+1)=0\) en \(y=0\). Er zijn daarom drie evenwichten: \((0,0)\), \((1,0)\) en \((-1, 0)\).

We zoeken nu uit wat voor evenwichten we hebben in dit stelsel differentiaalvergelijkingen. De algemene vorm van de Jabobi-matrix in \((x,y)\) is \[J(x,y) =\matrix{\dfrac{\partial (-x+x^3)}{\partial x} & \dfrac{\partial (-x+x^3)}{\partial y}\\ \dfrac{\partial (-2y)}{\partial x} & \dfrac{\partial (-2y)}{\partial y}}=\matrix{-1+3x^2 & 0\\ 0 & -2}\]

• De bijpassende linearisatie in \((0,0)\) is \[\cv{ x'\\ y'}=\matrix{-1 & 0\\ 0 & -2}\cv{x\\ y}\] De eigenwaarden van de Jabobi-matrix zijn negatief en dus gaan in de buurt van \((0,0)\) alle oplossingen naar de oorsprong toe. Het is een aantrekkend evenwicht.
• De bijpassende linearisatie in \((\pm 1,0)\) is \[\cv{ x'\\ y'}=\matrix{2 & 0\\ 0 & -2}\cv{x\\ y}\] De eigenwaarden van de Jabobi-matrix zijn positief en negatief en dus is \((\pm 1,0)\) een zadelpunt, in de zin dat in de ene richting oplossingskrommen naar het evenwicht gaan maar in de andere richting er vandaan.

Omdat de differentiaalvergelijkingen ontkoppeld zijn, dat wil zeggen twee eerste-orde GDVs die los van elkaar opgelost kunnen worden, is de analyse evenvoudig te checken: in de \(y\)-richting gaan alle oplossingen naar \(y=0\) toe en in de \(x\)-richting heeft het 1-dimensionale faseportret een aantrekkend evenwicht in \(x=0\) en twee afstotende evenwichten in \(x=-1\) en \(x=1\). Het 2-dimensionale faseportret kan als volgt geschetst worden.

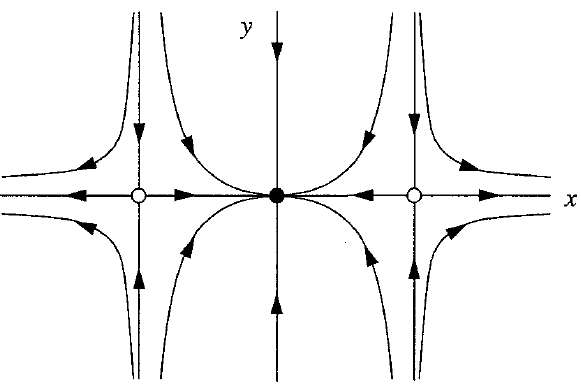
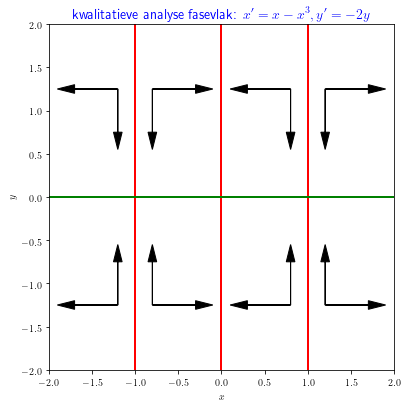
In kwalitatieve zin kun je het volgende richtingendiagram bepalen:

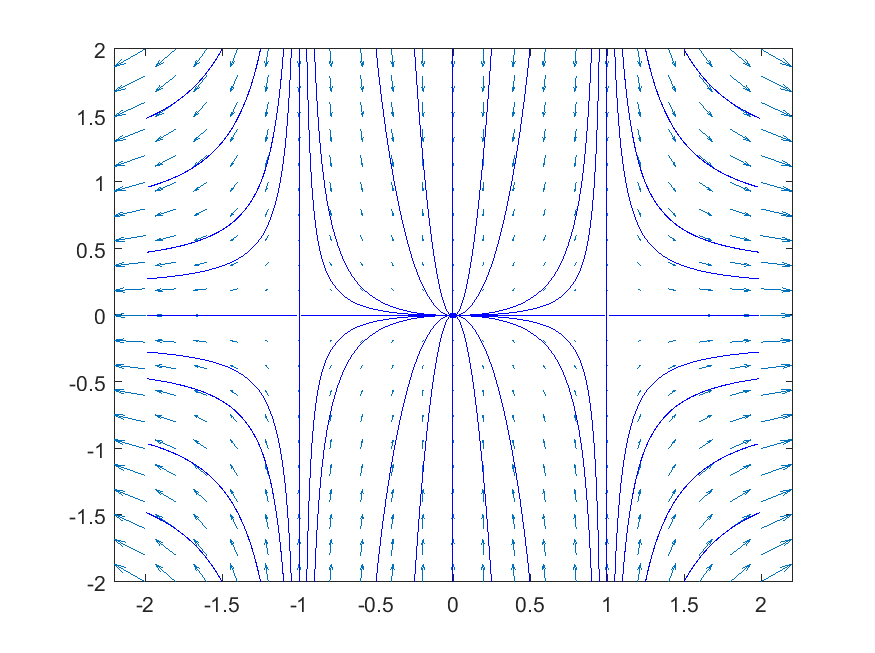
Dit stemt overeen met het faseportret getekend m.b.v. MATLAB.

>> [x,y] = meshgrid(-2:0.2:2, -2:0.2:2);
>> dxdt = -x+x.^3;
>> dydt = -2*y;
>> figure
>> quiver(x, y, dxdt, dydt), axis tight  % teken vectorveld
>> startx = [-1.5 -1.25 -1.1 -1.05 -1 -0.95 -0.9 -0.5 -0.25 0 0.25 0.5 0.9 0.95 1 1.05 1.1 1.25 1.5];
>> starty = -2*ones(size(startx));
>> streamline(x, y, dxdt, dydt, startx, starty)
>> starty = 2*ones(size(startx));
>> streamline(x, y, dxdt, dydt, startx, starty)
>> startx = [-1.01 -.99 0.99 1.01];
>> starty = [0 0 0 0];
>> streamline(x, y, dxdt, dydt, startx, starty)