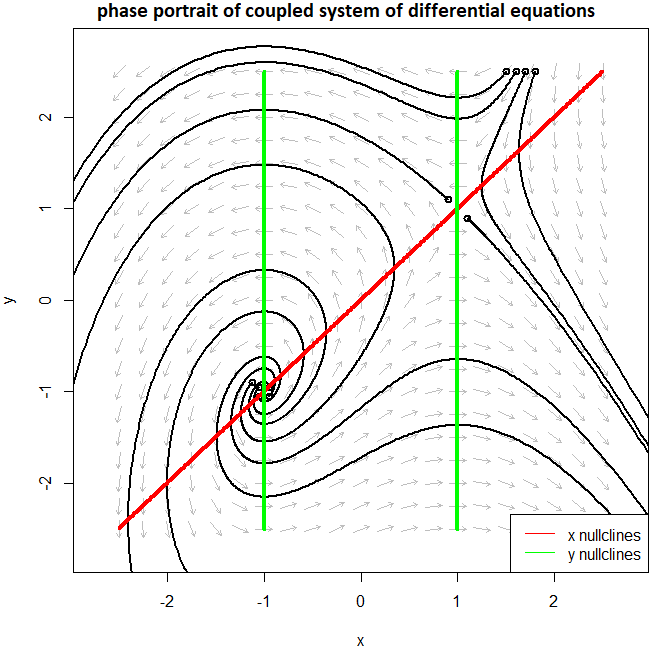
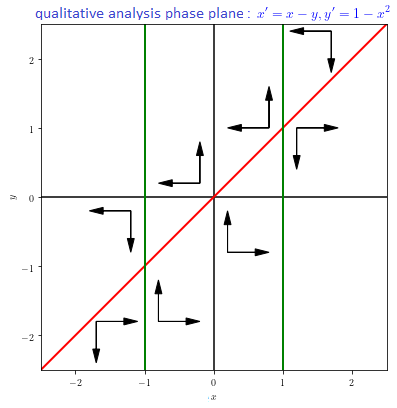
We consider the system of differential equations

$$\left\{\begin{aligned} \dfrac{\dd x}{\dd t} &=x-y\\[0.25cm] \dfrac{\dd y}{\dd t} &= 1-x^2 \end{aligned}\right.$$ Equilibria exist for $\dfrac{\dd x}{\dd t}=0$ and $\dfrac{\dd y}{\dd t}=0$, so when $x-y=0$ and $1-x^2=0$. Therefore, there are two equilibria: $(1,1)$ and $(-1,-1)$.

The diagram of directions looks like as follows:

We now explore the nature of the equilibria in this system of differential equations. The general form of the Jacobian matrix in $(x,y)$ is

$$J(x,y) =\matrix{\dfrac{\partial (x-y)}{\partial x} & \dfrac{\partial (x-y)}{\partial y}\\ \dfrac{\partial (1-x^2)}{\partial x} & \dfrac{\partial (1-x^2)}{\partial y}}=\matrix{1 & -1\\ -2x & 0}$$

• The corresponding linearization in $(1,1)$ is $$\cv{ x'\\ y'}=\matrix{1 & -1\\ -2 & 0}\cv{x\\ y}$$ For the computation of the eigenvalues of the Jacobian matrix we need to calculate the zeros of the characteristic polynomial of the matrix. This polynomial is $$\det\matrix{\lambda -1 & 1\\ 2 & \lambda}=(\lambda -1 )\lambda -2=\lambda^2-\lambda-2= (\lambda - 2)(\lambda+1)$$ and the zeros are $\lambda=-1$ and $\lambda=2$. We have a positive and negative eigenvalue and therefore $(1,1)$ is a saddle point.
• The corresponding linearization in $(-1,-1)$ is $$\cv{ x'\\ y'}=\matrix{1 & -1\\ 2 & 0}\cv{x\\ y}$$ For the computation of the eigenvalues of the Jacobian matrix we need to calculate the zeros of the characteristic polynomial of the matrix. This polynomial is $$\det\matrix{\lambda -1 & 1\\ -2 & \lambda}=(\lambda -1 )\lambda +2=\lambda^2-\lambda +2$$ and the zeros are $\lambda=\frac{1\pm\sqrt{1-4\cdot 2}}{2}= \frac{1}{2}\pm\frac{1}{2}\sqrt{7}\ii$. We have complex eigenvalues with a positive real part. Thus, $(-1,-1)$ is an equilibrium with expanding spirals in its neighbourhood as solution curves.

The above analysis is illustrated in the phase portrait below with some solution curves.