We bekijken het stelsel differentiaalvergelijkingen \[\left\{\begin{aligned} \dfrac{\dd x}{\dd t} &=x-y\\[0.25cm] \dfrac{\dd y}{\dd t} &= 1-x^2 \end{aligned}\right.\] Evenwichten zijn er als \(\dfrac{\dd x}{\dd t}=0\) en \(\dfrac{\dd y}{\dd t}=0\), dus als \(x-y=0\) en \(1-x^2=0\). Er zijn daarom twee evenwichten: \((1,1)\) en \((-1,-1)\).

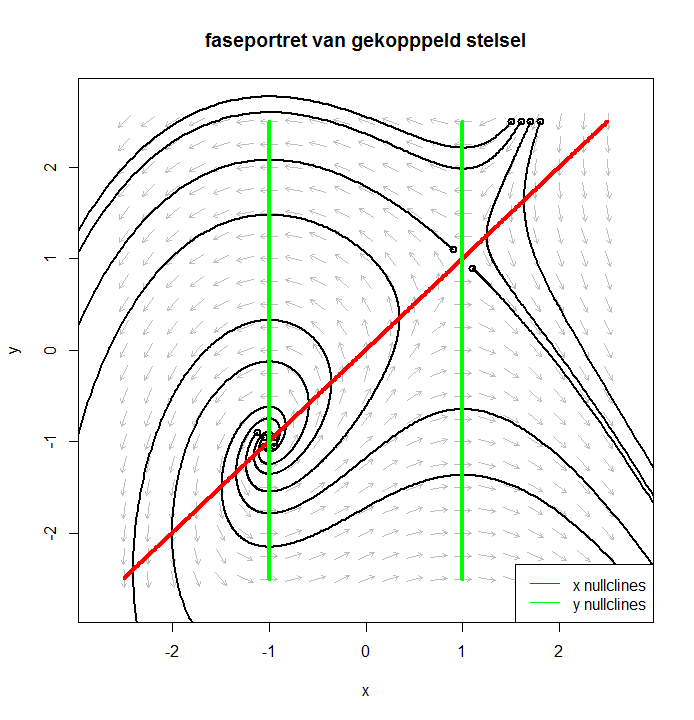
Het richtingendiagram ziet er als volgt uit:

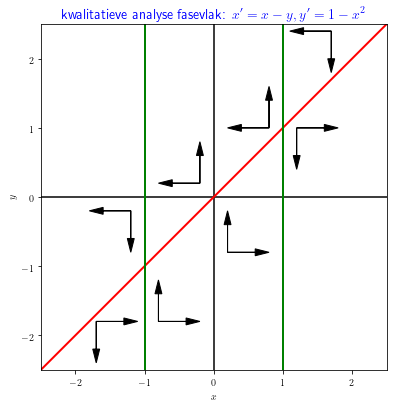
We zoeken nu uit wat voor evenwichten we hebben in dit stelsel differentiaalvergelijkingen. De algemene vorm van de Jacobi-matrix in \((x,y)\) is \[J(x,y) =\matrix{\dfrac{\partial (x-y)}{\partial x} & \dfrac{\partial (x-y)}{\partial y}\\ \dfrac{\partial (1-x^2)}{\partial x} & \dfrac{\partial (1-x^2)}{\partial y}}=\matrix{1 & -1\\ -2x & 0}\]

• De bijpassende linearisatie in \((1,1)\) is \[\cv{ x'\\ y'}=\matrix{1 & -1\\ -2 & 0}\cv{x\\ y}\] Om de eigenwaarden van de Jacobi-matrix uit te rekenen moeten we de nulpunten van de karakteristieke veelterm van de matrix berekenen. De veelterm is \[\det\matrix{\lambda -1 & 1\\ 2 & \lambda}=(\lambda -1 )\lambda -2=\lambda^2-\lambda-2= (\lambda - 2)(\lambda+1)\] De nulpunten zijn \(\lambda=-1\) en \(\lambda=2\). We hebben een positief en negatief nulpunt en daarom is \((1,1)\) een zadelpunt.
• De bijpassende linearisatie in \((-1,-1)\) is \[\cv{ x'\\ y'}=\matrix{1 & -1\\ 2 & 0}\cv{x\\ y}\] Om de eigenwaarden van de Jacobi-matrix uit te rekenen moeten we de nulpunten van de karakteristieke veelterm van de matrix berekenen. De veelterm is \[\det\matrix{\lambda -1 & 1\\ -2 & \lambda}=(\lambda -1 )\lambda +2=\lambda^2-\lambda +2\] De nulpunten zijn \(\lambda=\frac{1\pm\sqrt{1-4\cdot 2}}{2}= \frac{1}{2}\pm\frac{1}{2}\sqrt{7}\ii\). We hebben complexe nulpunten met een positief reëel deel. Dus is \((-1,-1)\) een evenwicht met uitdijende spiralen in de buurt als oplossingskrommen.

Onderstaande figuur toont het faseportret met enkele oplossingskrommen.