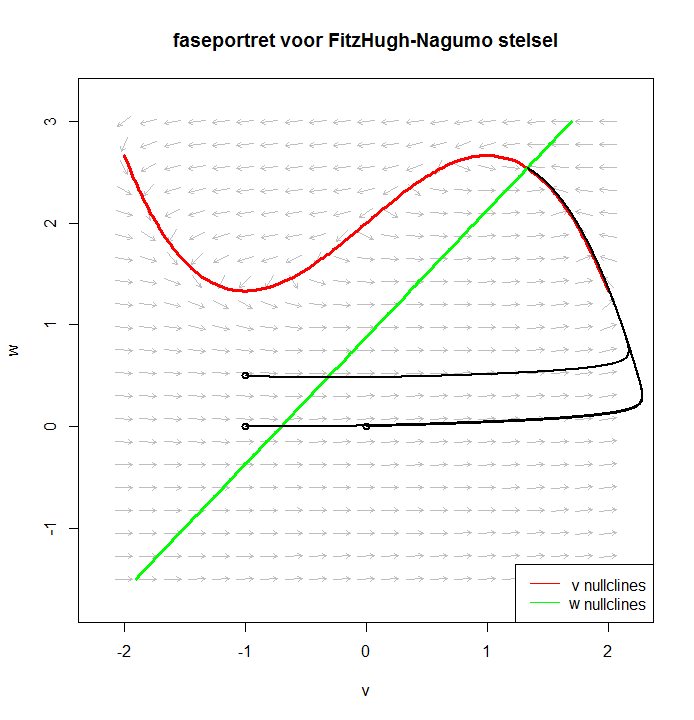
Geen stimulus Stel \[\begin{aligned}\frac{{\dd v}}{{\dd t}} &= f(v) - w \\[0.25cm] \frac{{\dd w}}{{\dd t}} &= \varepsilon \cdot (v + \beta - \gamma \cdot w)\end{aligned}\] Om het faseportret te kunnen tekenen en begrijpen, kijken we naar de \(v\)-isoclienen, dat wil zeggen de punten in het \(w-v\) vlak waarvoor \(v'=0\), oftewel de vectorpijlen in het vectorveld verticaal lopen. Dit is de grafiek van de derdegraadsfunctie \(w=f(v)=v - {\tfrac{1}{3}}{v^3}\). Ook kijken we naar de \(w\)-isoclienen, dat wil zeggen naar de punten in het \(v-w\) vlak waarvoor \(w'=0\), oftewel de vectorpijlen in het vectorveld horizontaal lopen. Dit is rechte lijn met vergelijking \(v + \beta - \gamma \cdot w\), oftewel de grafiek van de lineaire functie \(w = \frac{1}{\gamma}v + \frac{\beta}{\gamma}\). Deze nul-isoclienen zijn in onderstaand faseportret getekend om te laten zien dat een oplossingskrommen de \(v\)-nul-isocline nadert. Het evenwicht van dit niet-lineair stelsel vindt je door het snijpunt van de twee grafieken te bepalen, dat wil zeggen, door het stelsel \(\{w=f(v), w = \frac{1}{\gamma}v + \frac{\beta}{\gamma}\}\) op te lossen. Met de gegeven parameterwaarden voor \(\beta\) en \(\gamma\) is er een evenwicht bij \((v,w)\approx (-1.2,-0.6)\). In onderstaande faseportret zijn oplossingskrommen getekend en deze naderen het evenwicht.

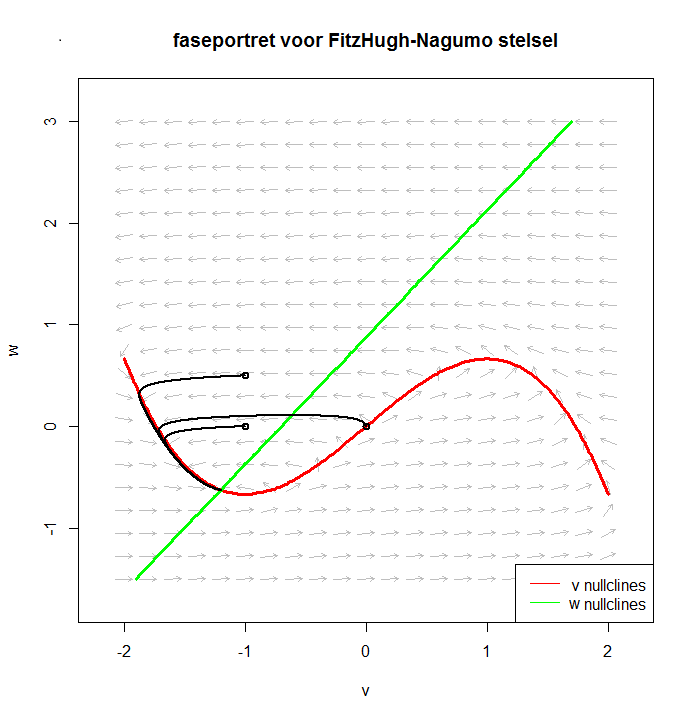
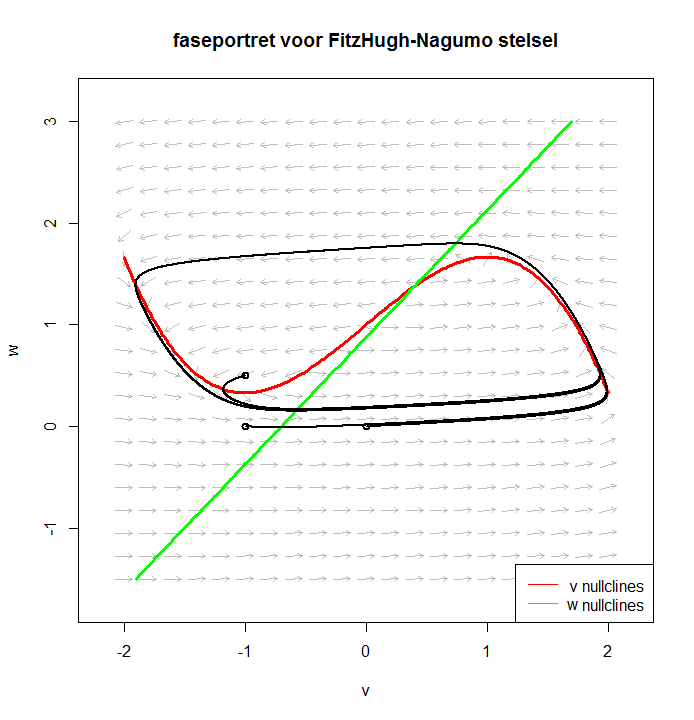
Wel een voldoende grote stroomstimulus Stel \[\begin{aligned}\frac{{\dd v}}{{\dd t}} &= f(v) - w +1 \\[0.25cm] \frac{{\dd w}}{{\dd t}} &= \varepsilon \cdot (v + \beta - \gamma \cdot w)\end{aligned}\] Om het faseportret te kunnen tekenen en begrijpen, kijken we naar de \(v\)-nul-isoclienen, dat wil zeggen de punten in het \(w-v\) vlak waarvoor \(v'=0\), oftewel de vectorpijlen in het vectorveld verticaal lopen. Dit is de grafiek van de derdegraadsfunctie \(w=f(v)=v - {\tfrac{1}{3}}{v^3}+1\). Dit is in feite de grafiek van de derdegraadskromme uit het eerdere voorbeeld verschoven in de verticale richting omhoog over een afstand 1. Ook kijken we naar de \(w\)-isoclienen, dat wil zeggen naar de punten in het \(v-w\) vlak waarvoor \(w'=0\), oftewel de vectorpijlen in het vectorveld horizontaal lopen. Dit is rechte lijn met vergelijking \(v + \beta - \gamma \cdot w\), oftewel de grafiek van de lineaire functie \(w = \frac{1}{\gamma}v + \frac{\beta}{\gamma}\). Dit is dezelfde rechte lijn als in het vorige voorbeeld. Deze nul-isoclienen zijn in onderstaand faseportret getekend om te laten zien dat een oplossingskrommen een limietcyclus nadert. Het evenwicht van dit niet-lineair stelsel vindt je door het snijpunt van de twee grafieken te bepalen, dat wil zeggen, door het stelsel \(\{w=f(v), w = \frac{1}{\gamma}v + \frac{\beta}{\gamma}\}\) op te lossen. Met de gegeven parameterwaarden voor \(\beta\) en \(\gamma\) is er een evenwicht bij \((v,w)\approx (0.4,1.4)\). In onderstaande faseportret is een oplossingskromme getekend en deze nader een limietcyclus, die rondom het evenwicht een periodieke baan is. Bij een constante, voldoende grote stimulus zal de membraanspanning een periodieke functie in tijd zijn.

Volledige analyse We bekijken nu de stabiliteit van het evenwicht als functie van stimulussterkte \(I\) voor het dynamische systeem \[\begin{aligned}\frac{{\dd v}}{{\dd t}} &= f(v) - w + {I_{{\rm{stim}}}} \\[0.25cm] \frac{\dd w}{\dd t} &= \varepsilon \cdot (v + \beta - \gamma \cdot w)\end{aligned}\] Als er geen stimulus is, dan is er een aantrekkend evenwicht. Als de stimulus \({I_{{\rm{stim}}}}\) klein genoeg is, dat wil zeggen, de grafiek van de derdegraadsfunctie maar zo weinig verticaal omhoog verschuift dat het snijpunt van de rechte lijn en de derdegraadskromme links van het minimum van de derdegraadsfunctie blijft, dan hebben we nog steeds een aantrekkend evenwicht. Pas wanneer de stimulus zodanig groot wordt dat het snijpunt tussen het lokale minimum en maximum komt te liggen, dan bewegen de oplossingen naar een limietcyclus rondom het evenwicht. Als de stimulus nog groter wordt (bijvoorbeeld \(I_{{\rm stim}}=1.5\) en het snijpunt rechts van het lokale maximum van de derdegraadsfunctie komt te liggen, dan wordt het evenwicht weer een aantrekkend evenwicht en hebben we te maken met een zogenaamde 'excitatie blokkade'.