Pencil-and-paper exercise set

Systems of differential equations: Non-linear differential equations

Pencil-and-paper exercise set

Exercise Consider the system of differential equations

$\left\{\begin{aligned} \dfrac{\dd x}{\dd t} &=x-2y\\[0.25cm] \dfrac{\dd y}{\dd t} &=4x-x^3 \end{aligned}\right.$ Determine the equilibria and their nature.

Worked-out solution

$\left\{\begin{aligned} \dfrac{\dd x}{\dd t} &=x-2y\\[0.25cm] \dfrac{\dd y}{\dd t} &=4x-x^3 \end{aligned}\right.$ In order to find the equilibria we must determine the solutions of the following system of equations

$\dfrac{\dd x}{\dd t}=0\quad\text{and}\quad \dfrac{\dd y}{\dd t}=0,$ that is

$x-2y=0\quad\text{and}\quad 4x-x^3=0$ We can determine these solutions as follows: in the second equation $4x-x^3=0$ we can place $x$ outside of brackets, and then the equation becomes $x(4-x^2)=0$ . The left-hand side can be factored into $x(2-x)(2+x)=0$ . So

$x=0,\quad x=2\quad\text{or}\quad x=-2$ If $x$ is known, then $y$ can be determined through $x-2y=0$ . We get as solutions of the system of equations

$(x,y)=(0,0),\quad (x,y)=(2,1)\quad\text{or}\quad (x,y)=(-2,-1)$

We now look at each equilibrium individually.

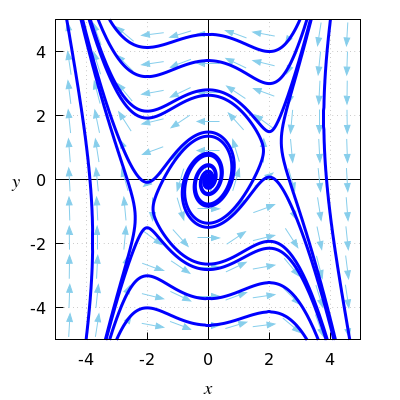
By local linearisation in the point $(0,0)$ we get the corresponding linear system of differential equations:

$\left\{\begin{aligned} \dfrac{\dd X}{\dd t} &=X-2Y\\[0.25cm] \dfrac{\dd Y}{\dd t} &=4X \end{aligned}\right.$ In matrix form, it looks like

$\cv{X'\\ Y'} = A\cdot\cv{X\\Y}\quad\text{with}\quad A=\matrix{1 & -2\\ 4 & 0}$ The characteristic polynomial of $A$ is equal to

$\begin{aligned}\det(A-\lambda\cdot I &= \det\matrix{1-\lambda & -2\\ 4 & -\lambda}\\[0.25cm] &=-\lambda\cdot(1-\lambda)-(-2)\cdot 4\\[0.25cm] &=\lambda^2-\lambda+8\\ \\ &= (\lambda-\tfrac{1}{2})^2+7\tfrac{3}{4}\end{aligned}$ The zeros of the quadratic polynomial can be found via the quadratic formula or by completing squares. The final form in which we have written the characteristic polynomial shows that we have complex zeros with positive real part, namely $\tfrac{1}{2}$ . From this it follows that $(0,0)$ is a repelling equilibrium with expanding spirals in the neighbourhood. This applies both to the initial system of differential equations and the corresponding linear system.

By local linearisation in the point $(2,1)$ and $(-2,-1)$ , respectively, we get the corresponding linear system of differential equations:

$\left\{\begin{aligned} \dfrac{\dd X}{\dd t} &=X-2Y\\[0.25cm] \dfrac{\dd Y}{\dd t} &=(4-3\cdot (\pm 2)^2)X=-8X \end{aligned}\right.$ In matrix form, it looks like

$\cv{X'\\ Y'} = A\cdot\cv{X\\Y}\quad\text{with}\quad A=\matrix{1 & -2\\ -8 & 0}$ The characteristic polynomial of $A$ is equal to

$\begin{aligned}\det(A-\lambda\cdot I &= \det\matrix{1-\lambda & -2\\ -8 & -\lambda}\\ \\ &=-\lambda\cdot(1-\lambda)-(-2)\cdot (-8)\\ \\ &=\lambda^2-\lambda-16\end{aligned}$ The zeros of the quadratic polynomial can be found via the quadratic formula or by completing squares. We get

$\lambda_{\pm}=\frac{1\pm\sqrt{1+4\cdot 16}}{2}=\frac{1\pm\sqrt{65}}{2}$ We have a positive and negative zero. It follows that $(2,1)$ and $(-2,-1)$ are both a saddle point. This applies both to the initial system of differential equations and the corresponding linear system.

The results of the analysis above is confirmed by the following phase portrait of the initial non-linear system of differential equations.

Exercise Consider the system of differential equations

$\left\{\begin{aligned} \dfrac{\dd x}{\dd t} &=a+x^2-y\\[0.25cm] \dfrac{\dd y}{\dd t} &=bx-cy \end{aligned}\right.$ with parameters $a$ , $b\ge 0,$ and $c>0$ . Determine the equilibria and their nature.

Worked-out solution

$\left\{\begin{aligned} \dfrac{\dd x}{\dd t} &=a+x^2-y\\[0.25cm] \dfrac{\dd y}{\dd t} &=bx-cy \end{aligned}\right.$ In order to find the equilibria we must determine the solutions of the following system of equations

$\dfrac{\dd x}{\dd t}=0\quad\text{and}\quad \dfrac{\dd y}{\dd t}=0$ that is

$a+x^2-y=0\quad\text{and}\quad bx-cy =0$ We can determine these solutions as follows. Isolate in each equation $y$ : $y=a+x^2$ and $y=\frac{b}{c}x$ . So we must determine the intersection(s) of a line through the origin with positive slope and a shifted quadratic polynomial in $x$ :

$x^2-\frac{b}{c}x+a=0$ The discriminant is equal to $\left(\frac{b}{c}\right)^2-4a$ .

If $D<0$ , i.e. $a>\left(\frac{b}{2c}\right)^2$ , then there is no solution of the system of equations and no equilibrium.

If $D>0$ , i.e. $a<\left(\frac{b}{2c}\right)^2$ , then there are two solutions and therefore exist two equilibria $\xi, \eta$ given by

$\xi=\frac{b}{2c}\pm\sqrt{\left(\frac{b}{2c}\right)^2-a}, \quad\eta=\frac{b}{c}\xi$

To get insight in the nature of these equilibria we determine the Jacobi matrix in a point $(x,y)$ :

$J(x,y)= \begin{pmatrix} \dfrac{\partial (a+x^2-y)}{\partial x} & \dfrac{\partial (a+x^2-y)}{\partial y}\\ \dfrac{\partial (bx-cy)}{\partial x} & \dfrac{\partial (bx-cy)}{\partial y}\end{pmatrix}=\begin{pmatrix}2x & -1 \\ b & -c\end{pmatrix}$
Now we use the local linearisation to a system of linear differential equations, and we use the trace and the determinant of the Jacobi matrix in the equilibria $\xi, \eta$ :

$\mathrm{sp}(J)=2\xi-c,\quad \det{J}=-2\xi+b=\mp\sqrt{b^2-4ac^2}$

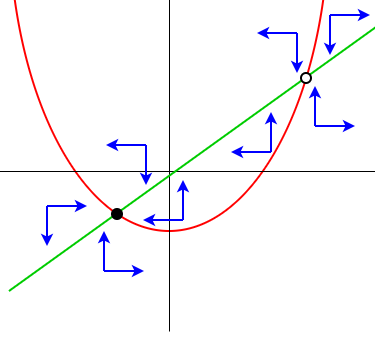
We consider the equilibrium $(\xi,\eta)=\Bigl(\frac{b}{2c}+\sqrt{\left(\frac{b}{2c}\right)^2-a}, \frac{b^2}{2c^2}+\frac{b}{c}\sqrt{\left(\frac{b}{2c}\right)^2-a}\Bigr)$ . Because $\det(J)(\xi,\eta)<0$ we always have a saddle point.

We consider the equilibrium $(\xi,\eta)=\Bigl(\frac{b}{2c}-\sqrt{\left(\frac{b}{2c}\right)^2-a}, \frac{b^2}{2c^2}-\frac{b}{c}\sqrt{\left(\frac{b}{2c}\right)^2-a}\Bigr)$ . Because $\det(J)(\xi,\eta)>0$ we always have a contect situation that is determined by the trace $\mathrm{sp}(J)(\xi,\eta)$ .

If $\mathrm{sp}(J)(\xi,\eta)<0$ , i.e. $\xi<\tfrac{1}{2}c$ , then we have an attractive equilibrium or inward spiralisation.

If $\mathrm{sp}(J)(\xi,\eta)>0$ , i.e. $\xi>\tfrac{1}{2}c$ , then we have a repelling equilibrium or outward spiralisation.

$\phantom{x}$
When you draw a directions diagram the above conclusions are confirmed. Below we draw the situation for a negative value of $a$ .