Pen-en-papier oefeningen

Stelsels van differentiaalvergelijkingen: Niet-lineaire differentiaalvergelijkingen

Pen-en-papier oefeningen

Bekijk het stelsel differentiaalvergelijkingen $\left\{\begin{aligned} \dfrac{\dd x}{\dd t} &=x-2y\\[0.25cm] \dfrac{\dd y}{\dd t} &=4x-x^3 \end{aligned}\right.$ Bepaal de evenwichten en hun aard.

$\left\{\begin{aligned} \dfrac{\dd x}{\dd t} &=x-2y\\[0.25cm] \dfrac{\dd y}{\dd t} &=4x-x^3 \end{aligned}\right.$ Om de evenwichten op te sporen moeten we de oplossingen van het volgende stelsel van vergelijkingen $\dfrac{\dd x}{\dd t}=0\quad\text{en}\quad \dfrac{\dd y}{\dd t}=0$ oftewel $x-2y=0\quad\text{en}\quad 4x-x^3=0$ Deze oplossingen kunnen we als volgt bepalen: in de tweede vergelijking $4x-x^3=0$ kunnen we $x$ buiten haakjes halen en dan wordt de vergelijking $x(4-x^2)=0$ . Het linkerlid is verder in factoren te ontbinden via een formule voor een merkwaardig product tot $x(2-x)(2+x)=0$ . Dus $x=0,\quad x=2\quad\text{of}\quad x=-2$ Als $x$ bekend is, dan is $y$ te bepalen via $x-2y=0$ . We krijgen als oplossingen van het stelsel vergelijkingen $(x,y)=(0,0),\quad (x,y)=(2,1)\quad\text{of}\quad (x,y)=(-2,-1)$

We bekijken nu elk evenwicht apart.

Door lokale linearisatie in het punt $(0,0)$ krijgen we het volgende bijpassende lineaire stelsel van differentiaalvergelijkingen: $\left\{\begin{aligned} \dfrac{\dd X}{\dd t} &=X-2Y\\[0.25cm] \dfrac{\dd Y}{\dd t} &=4X \end{aligned}\right.$ In matrixvorm ziet het er uit als $\cv{X'\\ Y'} = A\cdot\cv{X\\Y}\quad\text{met}\quad A=\matrix{1 & -2\\ 4 & 0}$ De karakteristieke veelterm van $A$ is gelijk aan $\begin{aligned}\det(A-\lambda\cdot I &= \det\matrix{1-\lambda & -2\\ 4 & -\lambda}\\ \\ &=-\lambda\cdot(1-\lambda)-(-2)\cdot 4\\ \\ &=\lambda^2-\lambda+8\\ \\ &= (\lambda-\tfrac{1}{2})^2+7\tfrac{3}{4}\end{aligned}$ Nulpunten van de kwadratische veelterm kunnen met de $abc$ -formule of via kwadraatafsplitsen berekend worden. De laatste vorm waarin we de karakteristieke veelterm geschreven hebben laat zien dat we te maken hebben met complexe nulpunten met een positief reëel deel, namelijk $\tfrac{1}{2}$ . Hieruit volgt van $(0,0)$ een afstotend evenwicht is met uitdijende spiralen in de omgeving. Dit geldt zowel voor het oorspronkelijk stelsel van differentiaalvergelijkingen als voor het bijpassende lineaire stelsel.

Door lokale linearisatie in het punt $(2,1)$ resp. $(-2,-1)$ krijgen we het volgende bijpassende lineaire stelsel van differentiaalvergelijkingen: $\left\{\begin{aligned} \dfrac{\dd X}{\dd t} &=X-2Y\\[0.25cm] \dfrac{\dd Y}{\dd t} &=(4-3\cdot (\pm 2)^2)X=-8X \end{aligned}\right.$ In matrixvorm ziet het er uit als $\cv{X'\\ Y'} = A\cdot\cv{X\\Y}\quad\text{met}\quad A=\matrix{1 & -2\\ -8 & 0}$ De karakteristieke veelterm van $A$ is gelijk aan $\begin{aligned}\det(A-\lambda\cdot I &= \det\matrix{1-\lambda & -2\\ -8 & -\lambda}\\[0.25cm] &=-\lambda\cdot(1-\lambda)-(-2)\cdot (-8)\\ \\ &=\lambda^2-\lambda-16\end{aligned}$ Nulpunten van de kwadratische veeltermen kunnen met de $abc$ -formule of via kwadraatafsplitsen berekend worden. We krijgen $\lambda_{\pm}=\frac{1\pm\sqrt{1+4\cdot 16}}{2}=\frac{1\pm\sqrt{65}}{2}$ We hebben dus te maken met een positief en negatief nulpunt. Hieruit volgt dat $(2,1)$ en $(-2,-1)$ beiden een zadelpunt zijn. Dit geldt zowel voor het oorspronkelijk stelsel van differentiaalvergelijkingen als voor het bijpassende lineaire stelsel.

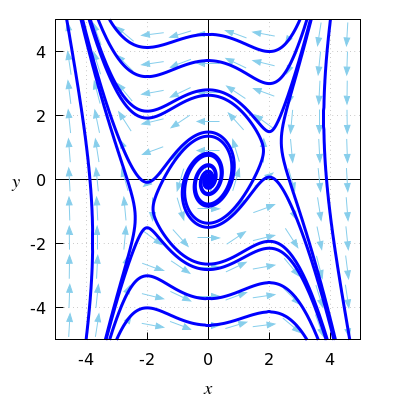
De resultaten van bovenstaande analyse wordt bevestigd in onderstaand faseportret van het gegeven niet-lineaire stelsel van differentiaalvergelijkingen.

Bekijk het stelsel differentiaalvergelijkingen $\left\{\begin{aligned} \dfrac{\dd x}{\dd t} &=a+x^2-y\\[0.25cm] \dfrac{\dd y}{\dd t} &=bx-cy \end{aligned}\right.$ met parameters $a$ willekeurig, $b\ge 0,$ en $c>0$ . Bepaal de evenwichten en hun aard.

$\left\{\begin{aligned} \dfrac{\dd x}{\dd t} &=a+x^2-y\\[0.25cm] \dfrac{\dd y}{\dd t} &=bx-cy \end{aligned}\right.$ Om de evenwichten op te sporen moeten we de oplossingen van het volgende stelsel van vergelijkingen $\dfrac{\dd x}{\dd t}=0\quad\text{en}\quad \dfrac{\dd y}{\dd t}=0$ oftewel $a+x^2-y=0\quad\text{en}\quad bx-cy =0$ Deze oplossingen kunnen we als volgt bepalen: in elke vergelijking kunnen we $y$ isoleren: $y=a+x^2$ en $y=\frac{b}{c}x$ . Het gaat dus om het bepalen van een snijpunt of meerdere snijpunten van een lijn door de oorsprong met positieve helling en een verschoven standaardveelterm, We krijgen de volgende kwadratische veelterm voor $x$ : $x^2-\frac{b}{c}x+a=0$
De discriminant is gelijk aan $\left(\frac{b}{c}\right)^2-4a$ .

Als $D<0$ , m.a.w. $a>\left(\frac{b}{2c}\right)^2$ , dan is er geen oplossing en bestaat er geen evenwicht.

Als $D>0$ , m.a.w. $a<\left(\frac{b}{2c}\right)^2$ , dan zijn er twee oplossingen en dus ook twee evenwichten $\xi, \eta$ gegeven door $\xi=\frac{b}{2c}\pm\sqrt{\left(\frac{b}{2c}\right)^2-a}, \quad\eta=\frac{b}{c}\xi$

Om inzicht te krijgen in de aard van deze evenwichten bepalen we de Jacobi-matrix in een punt $(x,y)$ :
$J(x,y)= \begin{pmatrix} \dfrac{\partial (a+x^2-y)}{\partial x} & \dfrac{\partial (a+x^2-y)}{\partial y}\\[0.25cm] \dfrac{\partial (bx-cy)}{\partial x} & \dfrac{\partial (bx-cy)}{\partial y}\end{pmatrix}=\begin{pmatrix}2x & -1 \\ b & -c\end{pmatrix}$
Voor inzicht in de aard van de evenwichten gebruiken we lokale linearisatie tot een stelsel van lineaire differentiaalvergeljkingen en gebruiken we het spoor en de determinant van de Jacobi-matrix in de evenwichten $\xi, \eta$ : $\mathrm{sp}(J)=2\xi-c,\quad \det{J}=-2\xi+b=\mp\sqrt{b^2-4ac^2}$

We kijken naar het evenwicht $(\xi,\eta)=\Bigl(\frac{b}{2c}+\sqrt{\left(\frac{b}{2c}\right)^2-a}, \frac{b^2}{2c^2}+\frac{b}{c}\sqrt{\left(\frac{b}{2c}\right)^2-a}\Bigr)$ . Omdat $\det(J)(\xi,\eta)<0$ hebben we altijd te maken met een zadelpunt.

We kijken naar het evenwicht $(\xi,\eta)=\Bigl(\frac{b}{2c}-\sqrt{\left(\frac{b}{2c}\right)^2-a}, \frac{b^2}{2c^2}-\frac{b}{c}\sqrt{\left(\frac{b}{2c}\right)^2-a}\Bigr)$ . Omdat $\det(J)(\xi,\eta)>0$ hebben we altijd te maken met een situatie die bepaald wordt door het spoor $\mathrm{sp}(J)(\xi,\eta)$ .

Als $\mathrm{sp}(J)(\xi,\eta)<0$ . d.w.z. als $\xi<\tfrac{1}{2}c$ , dan hebben we een aantrekkend evenwicht of krimpende spiralisering.

Als $\mathrm{sp}(J)(\xi,\eta)>0$ . d.w.z. als $\xi>\tfrac{1}{2}c$ , dan hebben we een afstotend evenwicht of uitdijende spiralisering.

$\phantom{x}$
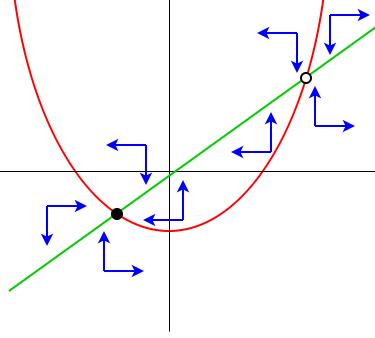
Als je een richtingendiagram tekent worden bovenstaande conclusies bevestigd. Hieronder hebben we een situatie met negatieve $a$ getekend.