Stelsels van differentiaalvergelijkingen: Lineaire stelsels van differentiaalvergelijkingen
 Faseportret tekenen in R
Faseportret tekenen in R
Het phaseR pakket biedt faciliteiten om een richtingsveld te tekenen voor een stelsel van differentiaalvergelijkingen en enkel oplossingskrommen hierin te tekenen. Onderstaande voorbeelden illustreren dit. Het hoeft niet te gaan om een stelsel van lineaire differentiaalvergelijkingen, maar we beperken ons hier wel tot dergelijke voorbeelden.
Twee positieve eigenwaarden \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= x+ 2 y\\[0.25cm] \frac{\dd y}{\dd t} &= 3y\end{aligned}\right.\]
>> library(phaseR)
>> model <- function(tijd, begintoestand, parameters){
with(as.list(c(begintoestand, parameters)),{
dxdt <- x + 2*y
dydt <- 3*y
return(list(c(dxdt, dydt)))
})
}
>> flowField(model, xlim = c(-1.5, 1.5), ylim = c(-1.5, 1.5),
system = "two.dim", state.names = c("x", "y"), points = 16,
add = FALSE, xlab ="x", ylab ="y", col="turquoise")
>> initvals <- matrix(c(-0.2,-0.1,-0.05,-0.001,-0.001,0.001,0.001,0.05,0.1,0.2,
0.001,0.001,0.001,0,-0.001,0.001,0,-0.001,-0.001,-0.001),
nrow=10, ncol=2, byrow=FALSE)
>> trajectory(model, y0 = initvals, tlim = c(0, 25),
state.names = c("x", "y"), lwd = 2, col="blue", cex = 0.1)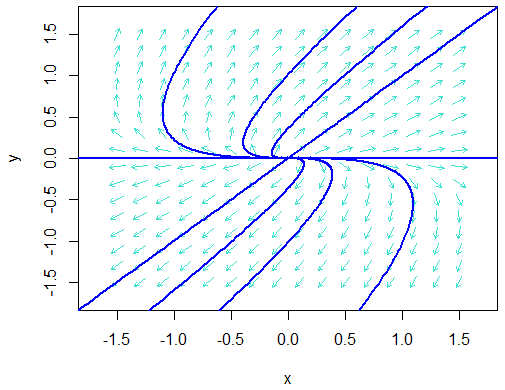
Twee negatieve eigenwaarden \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -2x-y\\[0.25cm] \frac{\dd y}{\dd t} &= -x - 2y\end{aligned}\right.\]
>> library(phaseR)
>> model <- function(tijd, begintoestand, parameters){
with(as.list(c(begintoestand, parameters)),{
dxdt <- -2*x - y
dydt <- -x - 2*y
return(list(c(dxdt, dydt)))
})
}
>> flowField(model, xlim = c(-1.5, 1.5), ylim = c(-1.5, 1.5),
system = "two.dim", state.names = c("x", "y"), points = 16,
add = FALSE, xlab ="x", ylab ="y", col="turquoise")
>> initvals <- matrix(c(-2, -1, 0, 1, 2, -2, -1, 0, 1, 2, -2, 2,
-2, -2, -2, -2, -2, 2, 2, 2, 2, 2, 0, 0),
nrow=12, ncol=2, byrow=FALSE)
>> trajectory(model, y0 = initvals, tlim = c(0, 25),
state.names = c("x", "y"), lwd = 2, col="blue", cex = 0.1)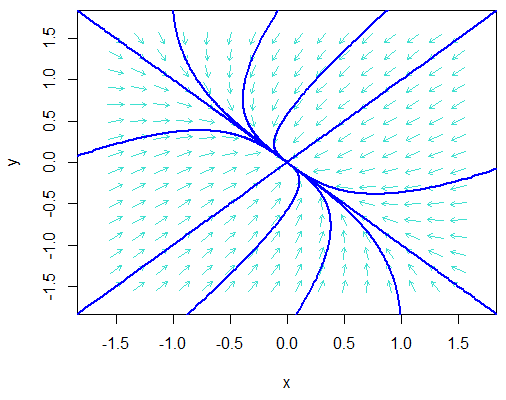
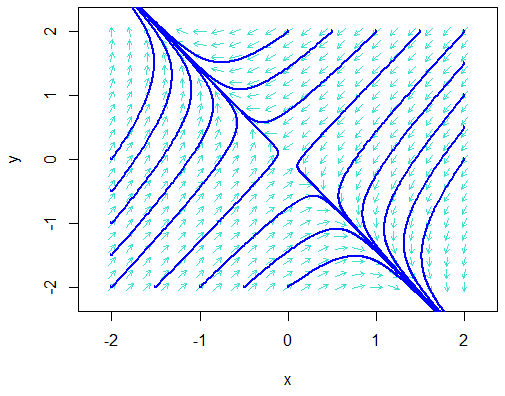
Een positieve en een negatieve eigenwaarde \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= -x-y\\[0.25cm] \frac{\dd y}{\dd t} &= -2x - y\end{aligned}\right.\]
>> library(phaseR)
>> model <- function(tijd, begintoestand, parameters){
with(as.list(c(begintoestand, parameters)),{
dxdt <- -x - y
dydt <- -2*x - yy
return(list(c(dxdt, dydt)))
})
}
>> flowField(model, xlim = c(-2, 2), ylim = c(-2, 2),
system = "two.dim", state.names = c("x", "y"), points = 21,
add = FALSE, xlab ="x", ylab ="y", col="turquoise")
>> initvals <- matrix(c(-2,-1.5,-1,-0.5,0,-2,-2,-2,-2,0,0.5,1,1.5,2,2,2,2,2,
-2,-2,-2,-2,-2,-1.5,-1,-0.5,0,2,2,2,2,2,1.5,1,0.5,0),
nrow=18, ncol=2, byrow=FALSE)
>> trajectory(model, y0 = initvals, tlim = c(0, 25),
state.names = c("x", "y"), lwd = 2, col="blue", cex = 0.1)