From a 2-dimensional system of homogeneous first-order linear GDVs to a homogeneous second-order linear GDV We consider the following system of coupled homogeneous first-order linear differential equations: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= a\, x+ b\, y\\[0.25cm] \frac{\dd y}{\dd t} &= c\, x + d\, y\end{aligned}\right.\] We can rewrite the system as a homogeneous second-order linear differential equation with constant coefficients for \(x(t)\) and a similar differential equation for \(y(t)\). This means that we can solve the system as a single differential equation!

Finding the corresponding ODE Let's see how this works for \(x(t)\). When we differentiate the left- and right-hand sides of the first equation in the system, we get \[\frac{\dd^2x}{\dd t^2}=a\frac{\dd x}{\dd t}+b\,\frac{\dd y}{\dd t}\] and after substitution of the second equation of the system we get \[\frac{\dd^2x}{\dd t^2}=a\frac{\dd x}{\dd t}+b\,c\,x + b\,d\,y\] The first equation of the system can also be written down as \(b\,y =\frac{\dd x}{\dd t}-a\, x\) and then substitution leads to the desired second- order ODE, which can be written as: \[ \frac{\dd^2x}{\dd t^2}-(a+d)\frac{\dd x}{\dd t}+(ad-bc)\,x =0\]

\(\phantom{abc}\)

We know how we can solve the above second-order ODE and that the behaviour of a solution depends on the discriminant of the corresponding characteristic polynomial \[\lambda^2 -(a+d)\lambda+(ad-bc)\] This discriminant \(D\) can be rewritten as: \[D=(a+d)^2-4(ad-bc)=(a-d)^2+4bc\] We can distinguish three cases:

1. If \((a-d)^2+4bc>0\) then there are two real roots of the characteristic polynomial: \[\lambda_{1,2}=\frac{a+d\pm\sqrt{(a-d)^2+4bc}}{2}\] and the general solution for \(x(t)\) is \[x(t)=c_1e^{\lambda_1t}+c_1e^{\lambda_2t}\]
2. If \((a-d)^2+4bc=0\) then there is one real root of the characteristic polynomial: \[\lambda=\frac{a+d}{2}\] and the general solution for \(x(t)\) is \[x(t)=(c_1+c_2 t)e^{\lambda t}\]
3. If \((a-d)^2+4bc<0\) then there are two complex roots of the characteristic polynomial: \[\lambda_{1,2}=\alpha\pm\mathrm{i}\,\beta\] with \[\alpha=\frac{a+d}{2}\quad\text{en}\quad\beta=\frac{\sqrt{-(a-d)^2-4bc}}{2}\] and the general solution for \(x(t)\) is \[x(t)=e^{\alpha t}\bigl(c_1\cos(\beta t)+c_2\sin(\beta t)\bigr)\]

\(\phantom{abc}\)

For \(y\) you can work it out in a similar manner.

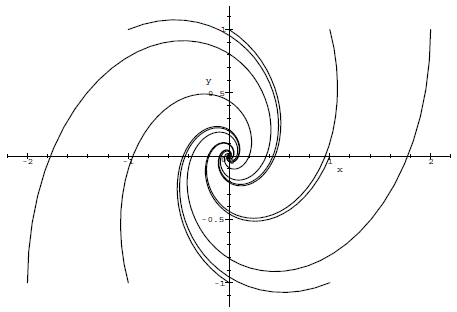
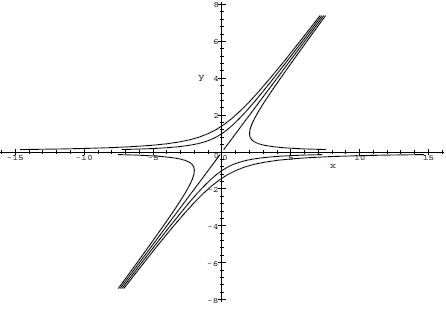
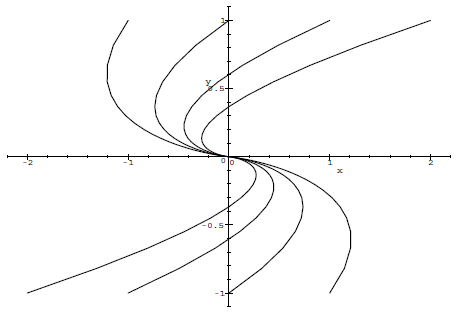
Solutions curves for a 2-dimensional system of 1st-order linear ODEs To get a better understanding of the behaviour of the solutions of the system of coupled homogeneous first-order linear differential equations one uses mostly the so-called phase portrait or phase plane. Then you draw parameter curves \( t\mapsto (x(t), y(t))\) for several initial conditions of the differential equation (and, if desired, the so-called direction field in the background; we omit this in the figures below). The solutions \(x(t)\) and \(y(t)\) are thus coordinate functions of a curve in the 2-dimensional plane. The solution curves give a good impression of the behaviour of the two solutions in one picture. Without proof, we show some figues with various types of phase portraits (the examples are not exhaustive and we also do not see in which direction the curves go).

• a negative and a positive real root of the characteristic polynomial:
  
• one real root of the characteristic polynomial:
  
• two complex roots of the characteristic polynomial: