The graph of a function \(f(x)\) in one variable is a curve in \(\mathbb{R}^2\) and the area under that graph on the interval \([a,b]\) is the definite integral \(\displaystyle \int_{a}^{b} f(x)\,\dd x\). We can also write this integral as \(\displaystyle \int_{[a,b]}f(x)\,\dd x\).

The graph of a function \(f(x,y)\) in two variables is a surface in \(\mathbb{R}^3\) and when the graph lies above a region \(R\) in the \(xy\) plane we can write the volume under that graph as the double integral \[\iint_R f(x,y)\,\dd(x,y)\] We will first limit ourselves to a rectangular area with sides parallel to the coordinate axes and in the case of a continuous and positive function \(f\), i.e., whose graph on \(R\) makes no jumps and lies above the \(xy\) plane, as in the figure below taken from the book Vervolgboek Wiskunde van Jan van de Craats with as function definition \[f(x,y)=\frac{1}{6}(x^2y+2\sqrt{x+1}-y^3+6)\quad\text{on the square }[0,2]\times [0,2]\text.\]

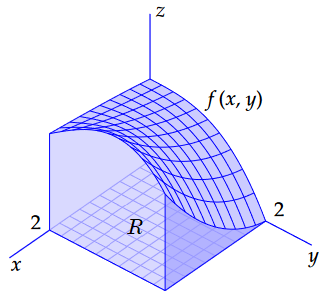
If there are parts where the function \(f(x,y)\) is negative, you can take its volume with a minus sign, just like integrals over a function in one variable, and thus extend the concept of volume to arbitrary continuous functions in two variables.

For a rectangle \(R=[a,b]\times [c,d]\), ie \(a\le x\le b\) and \(c\le y\le d\), we get for these volume \(V\) the iterated integration \[V = \int_{c}^{d}\left(\int_{a}^{b}f(x,y)\,\dd x\right)\!\dd y\] You can also do it the other way around (note the switching of the limits of integration) and for 'neat' functions (like our continuous function on a rectangle ) you get the same result: \[V= \int_{a}^{b}\left(\int_{c}^{d}f(x,y)\,\dd y\right)\!\dd x\] If you omit the parentheses, the symbol \(\dd x\,\dd y\) on the order of differentials points to 'integrate first to \(x\) and then to \(y\) '. The symbol \(\dd y\,\dd x\) then stands for 'first integrate to \(y\) and then to \(x\) '. In order to indicate even better for which variable the limits of integration have been specified, we will mention this in the following; this way you know exactly which values must be substituted in which variable.

In the next two theory pages we explain the double integral as iterated integration, after we have first looked at how a double integral can be numerically approximated with a Riemann sum.