De grafiek van een functie $f(x)$ in één veranderlijke is een kromme in $\mathbb{R}^2$ en de oppervlakte onder die grafiek op het interval $[a,b]$ is de bepaalde integraal $\displaystyle \int_{a}^{b} f(x)\,\dd x$. Deze integraal kunnen we ook noteren als $\displaystyle \int_{[a,b]}f(x)\,\dd x$.

De grafiek van een functie $f(x,y)$ in twee variabelen is een oppervlak in $\mathbb{R}^3$ en wanneer de grafiek boven een gebied $R$ in het $xy$-vlak ligt kunnen we de inhoud onder die grafiek noteren als de dubbelintegraal

$$\iint_R f(x,y)\,\dd(x,y)$$ We zullen ons eerst beperken tot een rechthoekig gebied met zijden evenwijdig aan de coördinaatassen en waarbij bovendien de functie $f$ continu en positief is, d.w.z. waarvan de grafiek ervan op $R$ geen sprongen maakt en boven het $xy$-vlak ligt, zoals in onderstaande figuur overgenomen uit het Vervolgboek Wiskunde van Jan van de Craats met als functiedefinitie $$f(x,y)=\frac{1}{6}(x^2y+2\sqrt{x+1}-y^3+6)\quad\text{op het vierkant }[0,2]\times [0,2]\text.$$

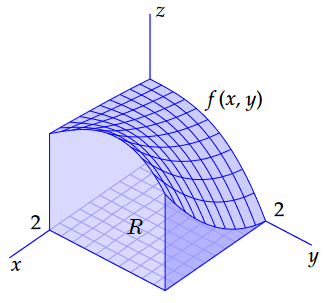
Als er stukken zijn waar de functie $f(x,y)$ negatief is, dan kun je de inhoud daarvan met een minteken nemen, net als bij integralen over een functie in één variabele, en zo het inhoudsbegrip uitbreiden naar willekeurige continue functies in twee variabelen.

Voor een rechthoek $R=[a,b]\times [c,d]$, d.w.z. $a\le x\le b$ en $c\le y\le d$, krijgen we voor deze inhoud $I$ dan de herhaalde integratie

$$I = \int_{c}^{d}\left(\int_{a}^{b}f(x,y)\,\dd x\right)\!\dd y$$ Je kunt het ook andersom doen (let op het verwisselen van de integratiegrenzen) en voor 'nette' functies (zoals onze continue functie op een rechthoek) krijg je dan hetzelfde resultaat: $$I= \int_{a}^{b}\left(\int_{c}^{d}f(x,y)\,\dd y\right)\!\dd x$$ Als je de haakjes weglaat wijst het symbool $\dd x\,\dd y$ op de volgorde van differentialen op 'eerst integreren naar $x$ en daarna naar $y$'. Het symbool $\dd y\,\dd x$ staat dan voor 'eerst integreren naar $y$ en daarna naar $x$'. Om nog beter aan te geven voor welke variabele de integratiegrenzen zijn opgegeven vermelden we dit in het vervolg; zo weet je precies welke waarden in welke variabele ingevuld moeten worden.

In de volgende twee theoriepagina's lichten we de dubbelintegraal als herhaalde integratie toe, nadat we eerst bekeken hebben hoe een dubbelintegraal numeriek met een Riemann-som benaderd kan worden.