Meervoudige integralen: Dubbelintegralen
 Dubbelintegralen benaderd met een Riemann-som
Dubbelintegralen benaderd met een Riemann-som
Hoe bereken je numeriek een dubbelintegraal? We gaan dit net zo aanpakken als bij numeriek integreren van functies in één veranderlijke. We doen het weer alleen voor een positieve continue functie \(f(x,y)\) gedefinieerd op een rechthoekig gebied \(R=[a,b]\times [c,d]\) ligt.
Aanpak met Riemann-sommen We verdelen hierbij steeds het interval \([a,b]\) op de \(x\)-as in \(m\) stukjes door in dat interval vaste punten \(x_0, x_1, x_2,\ldots, x_m\) aan te wijzen met \[a = x_0 < x_1 < x_2 < \cdots < x_m = b\tiny.\] Net zo verdelen we het interval \([c,d]\) op de \(y\)-as in \(n\) stukjes door in dat interval vaste punten \(y_0, y_1, y_2,\ldots, y_n\) aan te wijzen met \[c = y_0 < y_1 < y_2 < \cdots < y_n = d\tiny.\] Zo krijgen we \(m\times n\) deelrechthoekjes \(R_{ij}= [x_{i-1},x_i]\times [y_{i-1},y_i]\) met \(i=1,2,\ldots m\) en \(j=1,2,\ldots m\). Zo'n verzameling heet wel een verdeling \(\mathcal{V}\) van \([a,b]\times [c,d]\). Vervolgens kiezen we in elk van de deelrechthoekjes \(R_{ij}\) een strooipunt \(s_{ij}\). Dus \(x_{i-1}\le s_{ij}\le x_i\) voor \(i = 1, 2, \ldots m\) en \(y_{j-1}\le s_{ij}\le y_j\) voor \(j = 1, 2, \ldots n\) . De oppervlakte van elk van de deelrechthoekjes \(R_{ij}\) geven we aan met \({\vartriangle}_{ij}={\vartriangle}_{i}\cdot {\vartriangle}_{j}\), waarbij \({\vartriangle}_{i}=x_i-x_{i-1})\) en \({\vartriangle}_{j}=x_j-x_{j-1})\) de breedte en hoogte van elk deelrechthoekje \(R_{ij}\) zijn. Het maximum van de lengtes van de zijkanten van de deelrechthoekjes noemen we de maaswijdte. De uitdrukking \[S(\mathcal{V}; s_{11}, \ldots, s_{mn})=\sum_{i=1}^m\sum_{j=1}^{n}f(s_{ij})\cdot {\vartriangle}_{ij}\] heet een Riemann-som behorend bij de functie \(f\). Merk op: bij een gegeven verdeling \(\mathcal{V}\) van \([a, b]\times [c,d]\) horen veel verschillende Riemann-sommen: bij elke keuze van strooipunten krijg je er telkens een. Zo'n Riemann-som is dus de som van de inhouden van rechthoekige pilaartjes met de in de verdeling gebruikte deelrechthoekjes als grondvlakken. De inhouden van deze rechthoekige pilaartjes vormen opgeteld een benadering van de inhoud onder een grafiek die we willen berekenen. De gevraagde inhoud is in zekere zin een limiet van zulke Riemann-sommen. Zie onderstaand voorbeeld.
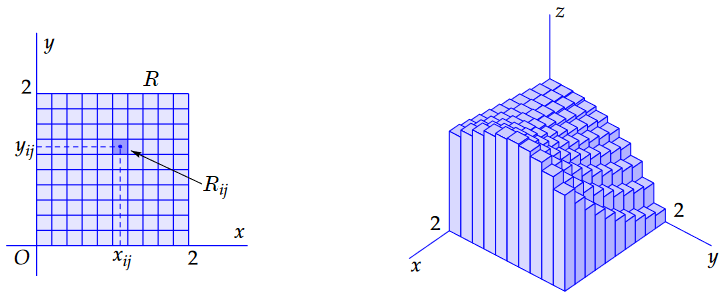
In bovenstaande figuur, voor de functie \(f(x,y)=\frac{1}{6}(x^2y+2\sqrt{x+1}-y^3+6)\), hebben we het vierkant \([0,2]\times[0,2]\) als integratiegebied \(R\), een gelijkmatige verdeling van \(R\) met \(10^2=100\) deelvierkantjes \(m=n=10\), \(\vartriangle_{i}=\vartriangle_{j}=0.2\) voor alle \(i,j=1,2,\ldots 10\) (de maaswijdte is gelijk aan \(0.2\)), en in elk deelvierkantje \(R_{ij}\) is voor \(s_{ij}\) het middelpunt ervan genomen. In acht significante cijfers krijgen we dan de Riemann-som \[\sum_{i=1}^{10}\sum_{j-1}^{10}f(s_{ij})\cdot {\vartriangle}_{ij} \approx 5.4251910\] Hoe kleiner de maaswijdte van de verdeling wordt, hoe beter de benadering. Als je bijvoorbeeld het vierkant gelijkmatig opdeelt in \(10^4=1000\) deelvierkantjes en de maaswijdte dus gelijk is aan \(0.02\), dan krijg je \[\sum_{i=1}^{100}\sum_{j-1}^{100}f(s_{ij})\cdot {\vartriangle}_{ij} \approx 5.4205590\] Doe je dat net zo met een maaswijdte van \(0.002\), dan krijg je \[\sum_{i=1}^{1000}\sum_{j-1}^{1000}f(s_{ij})\cdot {\vartriangle}_{ij} \approx 5.4205127\] en zijn de eerste zes decimalen al goed in vergelijk met het exacte resultaat \(\frac{29}9+4/3\sqrt{3}\approx 5.420512188\) voor de dubbelintegraal. Ook: \[\begin{aligned}\iint_R f(x,y)\,\dd(x,y) &= \lim_{n\to\infty}\left(\lim_{m\to\infty}f(s_{ij})\cdot {\vartriangle}_{i}\right)\cdot {\vartriangle}_{j}=\int_{y=0}^{y=2}\left(\int_{x=0}^{x=2}f(x,y)\,\dd x\right)\dd y\\[0.25cm] &= \lim_{m\to\infty}\left(\lim_{n\to\infty}f(s_{ij})\cdot {\vartriangle}_{j}\right)\cdot {\vartriangle}_{i}=\int_{x=0}^{x=2}\left(\int_{y=0}^{y=2}f(x,y)\,\dd y\right)\dd x\end{aligned}\]
Stappenplan voor een numerieke berekening van een dubbelintegraal Ook al zijn er veel betere methoden om een dubbelintegraal numeriek uit te rekenen, geeft de hierboven beschreven Riemann-integratiemethode wel een goed idee wat een dubbelintegraal nu eigenlijk is. We kunnen een wat breder toe te passen stappenplan opstellen:
- Verdeel het integratiegebied \(R\) in kleine deelgebiedjes \(\dd R\), die ook wel oppervlakte-elementjes genoemd worden.
- Kies de oppervlakte-elementjes zo klein dat de functie erboven bijna constant is.
- Kies een willekeurig punt \((x,y)\) in elk oppervlakte-elementje \(\dd R\) en bereken \(f(x,y)\). Vermenigvuldig dit met de oppervlakte \(|\dd R|\) van \(\dd R\).
- Tel alle uitkomsten verkregen in stap 3 bij elkaar op. De som is dan bij benadering gelijk aan de dubbelintegraal. De benadering is beter naarmate de oppervlakte-elementjes kleiner zijn.


