Multiple integrals: Double integrals
 Double integrals as iterated integrals
Double integrals as iterated integrals
In the previous theory pages it has already been suggested that a double integral can also be calculated exactly by repeated integration. We will get into this in a bit more detail.
Suppose that we want to calculate a double integral \[\iint_R f(x,y)\,\dd(x,y)\] for a positive continuous function \(f\) over a rectangular region of integration \(R=[a,b]\times [c,d]\). Define the following auxiliary function \[S(y)=\int_{x=a}^{x=b} f(x,y)\,\dd x\] With a fixed \(y\) you therefore integrate the function \(f(x,y)\) to \(x\).
Divide the region \(R\) into \(m\) strips of length \({\vartriangle}y=(d-c)/m\). In each strip, choose a horizontal line at height \(y_j\) and calculate \(S(y_j)\). This gives the area under the graph of \(f(x,y_j)\) and then the product of this with \({\vartriangle}y\) is equal to the volume of the `slice' with thickness \({\vartriangle}y\) that has the graph of the function \(f(x,y_j)\) as profile (\(x\) is the variable here, \(y_j\) is fixed).
In the figure below we have again chosen the function \(f(x,y)=\frac{1}{6}(x^2y+2\sqrt{x+1}-y^3+6)\) and the square \([0,2]\times[0,2]\) as region of integration \(R\). \(10\) horizontal strips have been taken ( \(m=10,{\vartriangle}y=0.2\) ). The 'slices' of which each height always fits the centre of the relevant strip can be seen on the right. 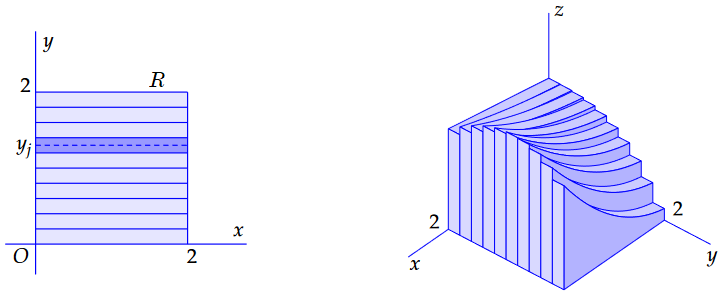
The area of that profile is \(S(y_j)\) and the sum \[\sum_{j=1}^{m}S(y_j)\cdot {\vartriangle}y\] is again an approximation of the double integral \(\iint_R f(x,y)\,\dd(x,y)\). At the same time it is also an approximation of the integral \(\int_{y=c}^{y=d} S(y)\,\dd y\). For 'neat' functions, both integrals are equal: \[\iint_R f(x,y)\,\dd(x,y)=\int_{y=c}^{y=d} S(y)\,\dd y= \int_{y=c}^{y=d}\left(\int_{x=a}^{x=b} f(x,y)\,\dd x\right)\dd y\]
In the example of the function \(f(x,y)=\frac{1}{6}(x^2y+2\sqrt{x+1}-y^3+6)\) and the square \([0,2]\times[0,2]\) as region of integration \(R\) we get \[\begin{aligned} S(y) &= \int_{x=0}^{x=2} f(x,y)\,\dd x\\[0.25cm] &= \int_{x=0}^{x=2}\frac{1}{6}(x^2y+2\sqrt{x+1}-y^3+6)\,\dd x \\[0.25cm] &=\Bigl[\frac{1}{18}x^3y+\frac{2}{9}(x+1)^{\frac{3}{2}}-\frac{1}{6}xy^3+x\Bigr]_0^{2}\\[0.25cm] &= \bigl(\frac{4}{9}y+\frac{2}{9}\sqrt{27}-\frac{1}{3}y^3+2\bigr)-\frac{2}{9}\\[0.25cm] &= \frac{4}{9}y+\frac{2}{3}\sqrt{3}-\frac{1}{3}y^3+\frac{16}{9}\end{aligned}\] and therefore \[\begin{aligned}\iint_R f(x,y)\,\dd(x,y) &= \int_{y=0}^{y=2} S(y)\,\dd y\\[0.25cm] &= \int_{y=0}^{y=2}\left(\frac{4}{9}y+\frac{2}{3}\sqrt{3}-\frac{1}{3}y^3+\frac{16}{9}\right)\dd y\\[0.25cm] &= \Bigl[\frac{2}{9}y^2+\frac{2}{3}\sqrt{3}y-\frac{1}{12}y^4+\frac{16}{9}y\Bigl]_{0}^{2}\\[0.25cm] &=\frac{8}{9} + \frac{4}{3}\sqrt{3}-\frac{16}{12}+\frac{32}{9}\\[0.25cm] &= \frac{28}{9}+\frac{4}{3}\sqrt{3}\end{aligned}\]
Changing the order of integration Above we first integrated to \(x\) and then to \(y\). But the order can also be reversed. The double integral then becomes \[\iint_R f(x,y)\,\dd(y,x)= \int_{x=a}^{x=b}\left(\int_{y=c}^{y=d} f(x,y)\,\dd y\right)\dd x\] The result of iterated integration is the same, but the route is different. In the derivation of this formula you now start with the introduction of the auxiliary function \[T(x)=\int_{y=c}^{y=d} f(x,y)\,\dd y\] With a fixed \(x\) you integrate the function \(f(x,y)\) to \(y\). After this you divide the region \(R\) into \(n\) vertical strips of length \({\vartriangle}x=(b-a)/n\). In each strip, choose a vertical line of width \(x_i\) and calculate \(T(x_i)\). This gives the area under the graph of \(f(x_i,y)\) and the product of this with \({\vartriangle}x\) is then equal to the volume of the `slice' with thickness \({\vartriangle}x\) that has the graph of the function \(f(x_i,y)\) as profile (\(y\) is the variable here, \(x_i\) is fixed). Below is the strip partition and the slices approximation of the double integral for the above example.
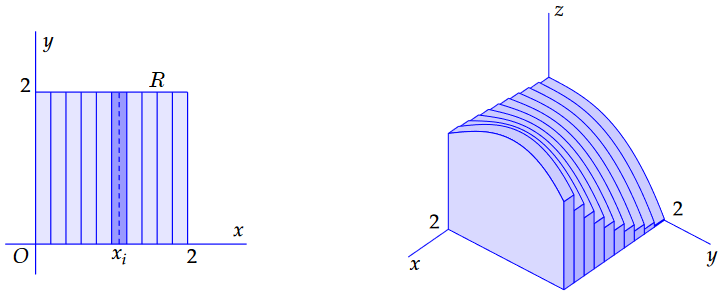
The area of the profile \(f(x_i,y)\) is \(T(x_i)\) and the sum \[\sum_{j=1}^{x=b}T(x_j)\cdot {\vartriangle}x\] is again an approximation of the double integral \(\iint_R f(x,y)\,\dd(y,x)\). At the same time it is also an approximation of the integral \(\int_{x=a}^{x=b} T(x)\,\dd x\). For 'neat' functions, both integrals are equal to each other: \[\iint_R f(x,y)\,\dd(y,x)=\int_{x=a}^{x=b} T(x)\,\dd x= \int_{x=a}^{x=b}\left(\int_{y=c}^{y=d} f(x,y)\,\dd y\right)\dd x\] To avoid using parentheses, the notation \(\dd(y,x)=\dd y\,\dd x\) is interpreted as repeated integration with first integrating to \(y\) and then integrating to \(x\). The notation \(\dd(x,y)=\dd x\,\dd y\) is the other way around: first integrate to \(x\) and only then integrate to \(y\). With 'neat' functions this produces the same result. Sometimes you have to make a well-considered choice of integration order because of the simplicity of the calculation.
\[\begin{aligned} \iint_R (1-x+y)\,\dd(x,y) &= \int_{y=1}^{y=3}\left(\int_{x=0}^{x=1}(1-x+y)\,\dd x\right)\dd y\\[0.25cm] &=\int_{y=1}^{y=3}\biggl[x-{{1}\over{2}}x^2+xy\biggr]_{x=0}^{x=1}\,\,\dd y\\[0.25cm] &= \int_{y=1}^{y=3}\left(y+{{1}\over{2}}\right)\dd y\\[0.25cm] &=\biggl[{{y^2}\over{2}}+{{y}\over{2}}\biggr]_{y=1}^{y=3}\\[0.25cm] &= 6-1\\[0.25cm] &=5\end{aligned}\]
You get the same result according to Fubini's theorem by reversing the integration variables: \[\begin{aligned} \iint_R (1-x+y)\,\dd(x,y) &= \int_{x=0}^{x=1}\left(\int_{y=1}^{y=3}(1-x+y)\,\dd y\right)\dd x\\[0.25cm] &=\int_{x=0}^{x=1}\biggl[y-xy+{{1}\over{2}}y^2\biggr]_{y=1}^{y=3}\,\,\dd x\\[0.25cm] &= \int_{x=0}^{x=1}\biggl(\bigl({{15}\over{2}}-3\,x\bigr)-\bigl({{3}\over{2}}-x\bigr)\biggr)\,\dd x\\[0.25cm] &= \int_{x=0}^{x=1}\left(6-2\,x\right)\dd x\\[0.25cm] &=\biggl[6\,x-x^2\biggr]_{x=0}^{x=1}\\[0.25cm] &= 6\times 1-1^2\\[0.25cm] &=5\end{aligned}\]


