Multiple integrals: Double integrals
 Double integrals over a bounded, but non-rectangular region
Double integrals over a bounded, but non-rectangular region
The region of integration in a double integral need not necessarily be a rectangle; this already follows from the interpretation that it is the volume under the graph of a positive continuous function \(f(x,y)\) over a closed region in the \(xy\) plane. We start with two particular regions, which are one-sidedly simple.
A y-simple region of integration A region of integration is \(\boldsymbol{y}\)-simple if it is bounded by two vertical lines \(x=a\) and \(x=b\) together with two continuous functions \(y=c(x)\) and \(y=d(x)\) between these two lines. The figure below illustrates the situation.
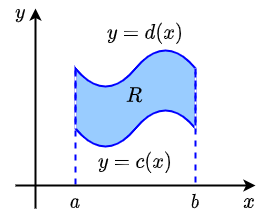
The double integral \(\displaystyle \iint_R f(x,y)\,\dd(x,y)\) is then approximated by adding the volumne under the graph of \(f\) of 'very thin' slices to the left starting in \(x\) and with width \(\dd x\) between \(x=a\) and \(x=b\), approximated by \(\displaystyle \left(\int_{y=c(x)}^{y=d(x)}f(x,y)\,\dd y\right)\!\cdot \dd x\). Thus, in the infinitesimal case, we get the following iterated integral: \[ \iint_R f(x,y)\,\dd(x,y)=\int_{x=a}^{x=b}\left(\int_{y=c(x)}^{y=d(x)}f(x,y)\,\dd y\right)\dd x\]
An x-simple region of integration A region of integration is \(\boldsymbol{x}\)-simple if it is bounded by two horizontal lines \(y=c\) and \(y=d\) together with two continuous functions \(x=a(y)\) and \(x=d(y)\) between these two lines. The figure below illustrates the situation.
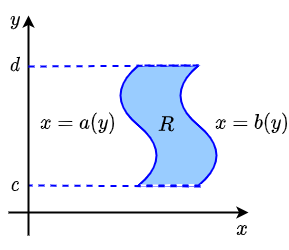
The double integral \(\displaystyle \iint_R f(x,y)\,\dd(x,y)\) is then approximated by adding the volumes under the graph of \(f\) of 'very thin' starting on the left in \(y\) and with height \(\dd y\) between \(y=c\) and \(y=d\), approximated by \(\displaystyle \left(\int_{x=a(y)}^{x=b(y)}f(x,y)\,\dd x\right)\!\cdot \dd y\). Thus, in the infinitesimal case, we get the following iterated integral: \[ \iint_R f(x,y)\,\dd(x,y)=\int_{y=c}^{y=d}\left(\int_{x=a(y)}^{x=b(y)}f(x,y)\,\dd x\right)\dd y\]
Many of the regions of integration over which we want to compute a double integral are \(y\)-easy, \(x\)-easy, or both. In the latter case, the following strong version of Fubini's theorem holds.
Strong Form of Fubini's Theorem Suppose \(f(x,y)\) is a continuous function on a region of integration \(R\)
- If \(R\) is \(y\)-simple, i.e. \(R=\{(x,y)\mid a\le x\le b, c(x)\le y\le d(x)\}\), with continuous function \(y=c(x)\) and \(y=d(x)\), then \[ \iint_R f(x,y)\,\dd(x,y)=\int_{x=a}^{x=b}\left(\int_{y=c(x)}^{y=d(x)}f(x,y)\,\dd y\right)\dd x\]
- If \(R\) is \(x\)-simple, i.e. \(R=\{(x,y)\mid a(x)\le x\le b(x), c\le y\le d\}\), with continuous function \(x=a(y)\) and \(x=b(y)\), then \[ \iint_R f(x,y)\,\dd(x,y)=\int_{y=c}^{y=d}\left(\int_{x=a(y)}^{x=b(y)}f(x,y)\,\dd x\right)\dd y\]
- If \(R\) is \(x\)- and \(y\)-simple, that is \[ R=\{(x,y)\mid a(x)\le x\le b(x), c\le y\le d\}\quad\text{and}\quad R=\{(x,y)\mid a\le x\le b, c(x)\le y\le d(x)\}\] for some continuous functions \(x=a(y)\), \(x=b(y)\), \(y=c(x)\) and \(y=d(x)\), then \[ \iint_R f(x,y)\,\dd(x,y)=\int_{x=a}^{x=b}\left(\int_{y=c(x)}^{y=d(x)}f(x,y)\,\dd y\right)\dd x=\int_{y=a}^{y=b}\left(\int_{x=a(y)}^{x=b(y)}f(x,y)\,\dd x\right)\dd y\]
\(\iint_R (3x+y)\,\dd(x,y)={}\) \({{3}\over{5}}\)
The parabolas \(y=x^2\) and \(x=y^2\) intersect at the origin and at the point \((1,1)\). If we consider the region of integration as a \(y\)-simple region, then we first keep \(x\) fixed (with \(0\le x\le 1\) and integrate for this fixed \(x\) to \(y\). The integration limits are then \(a(y)=x^2\) and \(b(y)=\sqrt{x}\); see the figure below.
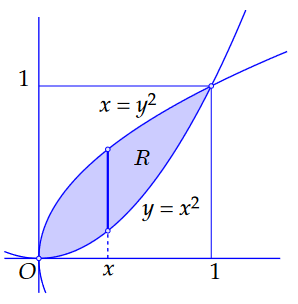
The iterated integral becomes: \[\begin{aligned}\iint_R (3 x+y)\,\dd(x,y) &= \int_{x=0}^{x=1}\left(\int_{y=x^2}^{y=\sqrt{x}}(3 x+y)\,\dd y\right)\dd x\\[0.25cm] &= \int_{x=0}^{x=1}\biggl[(3 xy+{{1}\over{2}} y^2)\biggr]_{y=x^2}^{y=\sqrt{x}}\,\dd x\\[0.25cm] &= \int_{x=0}^{x=1}\bigl((3 x^{\frac{3}{2}}+{{1}\over{2}} x)-(3 x^3+{{1}\over{2}} x^4)\bigr)\,\dd x\\[0.25cm] &=\biggl[{{6}\over{5}} x^{\frac{5}{2}}+{{1}\over{4}}x^2-{{3}\over{4}} x^4-{{1}\over{10}} x^5\biggr]_{x=0}^{x=1}\\[0.25cm] &= {{6}\over{5}}+{{1}\over{4}}-{{3}\over{4}}-{{1}\over{10}}\\[0.25cm]&={{3}\over{5}} \end{aligned}\]
We can also consider the region of integration as \(x\)-simple. Then we first keep \(y\) fixed (with \(0\le y\le 1\) and integrate for this fixed \(y\) to \(x\). The integration limits are then \(c(x)=y^2\) and \(d(x)=\sqrt{y}\); see the figure below.
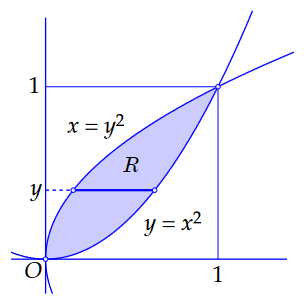
The iterated integral becomes: \[\begin{aligned}\iint_R (3 x+y)\,\dd(x,y) &= \int_{y=0}^{y=1}\left(\int_{x=y^2}^{x=\sqrt{y}}(3x+y)\,\dd x\right)\dd y\\[0.25cm] &= \int_{y=0}^{y=1}\biggl[({{3}\over{2}} x^2+xy)\biggr]_{x=y^2}^{x=\sqrt{y}}\,\dd x\\[0.25cm] &= \int_{y=0}^{y=1}\bigl(({{3}\over{2}} y+y^{\frac{3}{2}})-({{3}\over{2}} y^4+y^3)\bigr)\,\dd x\\[0.25cm] &=\biggl[{{3}\over{4}} y^2+{{2}\over{5}} y^{\frac{5}{2}}-{{3}\over{10}} y^5-{{1}\over{4}} y^4\biggr]_{y=0}^{y=1}\\[0.25cm] &= {{3}\over{4}}+{{2}\over{5}}-{{3}\over{10}}-{{1}\over{4}}\\[0.25cm]&={{3}\over{5}} \end{aligned}\]
The route is different, but the result is the same.
Approach for calculating a double integral In the exact calculation of a double integral \(\iint_R f(x,y)\dd(x,y)\) over a non-rectangular region \(R\) you can proceed as follows.
- Sketch the region \(R\) in the \(xy\) plane.
- Check whether the region of integration is \(x\)-simple, \(y\)-simple, or maybe both.
- Decide on the basis of the integrand and the nature of the region of integration whether to integrate to \(x\) or \(y\) first.
When integrating first to \(y\) (i.e. \(R\) is \(y\)-simple):
- Determine the left bound \(a\) and right bound \(b\) for \(x\) as extremes of \(R\) in the horizontal direction.
- Draw a vertical auxiliary line at position \(x\) between \(a\) and \(b\) in the sketch of \(R\)
- Determine the lower limit \(c(x)\) and the upper limit \(d(x)\) for the segment that remains within \(R\) at horizontal position \(x\)
- Calculate \(\displaystyle \int_{y=c(x)}^{y=d(x)}\,f(x,y)\,\dd y\). This is a function of \(x\).
- Integrate the latter function with limits of integration \(a\) and \(b\). So: \[\iint_R f(x,y)\,\dd(x,y)=\int_{x=a}^{x=b}\left(\int_{y=c(x)}^{y=d(x)}f(x,y)\,\dd y\right)\dd x\]
When integrating first to \(x\) (i.e. \(R\) is \(x\) -simple):
- Determine the \(c\) lower bound and \(d\) upper bound for \(y\) as extremes of \(R\) in the vertical direction.
- Draw a horizontal auxiliary line at position \(y\) between \(c\) and \(d\) in the sketch of \(R\)
- Determine the left limit \(a(y)\) and the right limit \(b(y)\) for the segment that remains within \(R\) at vertical position \(y\)
- Calculate \(\displaystyle \int_{x=a(y)}^{x=d(y)} f(x,y)\,\dd x\). This is a function of \(y\).
- Integrate the latter function with limits of integration \(c\) and \(d\). So: \[\iint_R f(x,y)\, \dd(x,y)=\int_{y=c}^{y=d}\left(\int_{x=a(y)}^{x=b(y)} f(x,y)\,\dd x\right)\dd y\]


