Meervoudige integralen: Dubbelintegralen
Dubbelintegralen over een begrensd maar niet-rechthoekig gebied
Het integratiegebied bij een dubbelintegraal hoeft niet per se een rechthoek te zijn; dit volgt al uit de interpretatie dat het de inhoud onder de grafiek van een positieve continue functie \(f(x,y)\) boven een gesloten gebied in het \(xy\)-vlak iss. We beginnen met twee bijzondere gebieden, die eenzijdig eenvoudig zijn.
Een y-eenvoudig integratiegebied Een integratiegebied is \(\boldsymbol{y}\)-eenvoudig als het begrensd wordt door twee verticale lijnen \(x=a\) en \(x=b\) samen met twee continue functies \(y=c(x)\) en \(y=d(x)\) tussen deze twee lijnen, Onderstaande figuur schetst de situatie.
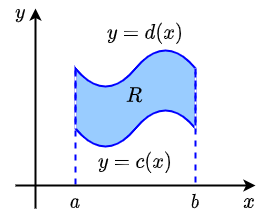
De dubbelintegraal \(\displaystyle \iint_R f(x,y)\,\dd(x,y)\) wordt dan benaderd door de inhouden onder de grafiek van \(f\) van 'zeer dunne' plakjes links startend in \(x\) en met breedte \(\dd x\) tussen \(x=a\) en \(x=b\), benaderd met \(\displaystyle \left(\int_{y=c(x)}^{y=d(x)}f(x,y)\,\dd y\right)\!\cdot \dd x\), bij elkaar op te tellen. Daarmee krijgen we in het infinitesimale geval de volgende herhaalde integraal: \[ \iint_R f(x,y)\,\dd(x,y)=\int_{x=a}^{x=b}\left(\int_{y=c(x)}^{y=d(x)}f(x,y)\,\dd y\right)\dd x\]
Een x-eenvoudig integratiegebied Een integratiegebied is \(\boldsymbol{x}\)-eenvoudig als het begrensd wordt door twee horizontale lijnen \(y=c\) en \(y=d\) samen met twee continue functies \(x=a(y)\) en \(x=d(y)\) tussen deze twee lijnen, Onderstaande figuur schetst de situatie.
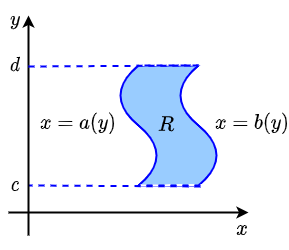
De dubbelintegraal \(\displaystyle \iint_R f(x,y)\,\dd(x,y)\) wordt dan benaderd door de inhouden onder de grafiek van \(f\) van 'zeer dunne' plakjes onder startend in \(y\) en met hoogte \(\dd y\) tussen \(y=c\) en \(y=d\), benaderd met \(\displaystyle \left(\int_{x=a(y)}^{x=b(y)}f(x,y)\,\dd x\right)\!\cdot \dd y\), bij elkaar op te tellen. Daarmee krijgen we in het infinitesimale geval de volgende herhaalde integraal: \[ \iint_R f(x,y)\,\dd(x,y)=\int_{y=c}^{y=d}\left(\int_{x=a(y)}^{x=b(y)}f(x,y)\,\dd x\right)\dd y\]
Veel van de integratiegebieden waarover we een dubbelintegraal willen berekenen zijn \(y\)-eenvoudig, \(x\)-eenvoudig, of allebei. In het laatste geval geldt de volgende sterke versie van de stelling van Fubini.
Sterke stelling van Fubini Stel dat \(f(x,y)\) een continue functie is op een integratiegebied \(R\)
- Als \(R\) \(y\)-eenvoudig is, d.w.z. \(R=\{(x,y)\mid a\le x\le b, c(x)\le y\le d(x)\}\), met continue functie \(y=c(x)\) en \(y=d(x)\), dan geldt:\[ \iint_R f(x,y)\,\dd(x,y)=\int_{x=a}^{x=b}\left(\int_{y=c(x)}^{y=d(x)}f(x,y)\,\dd y\right)\dd x\]
- Als \(R\) \(x\)-eenvoudig is, d.w.z. \(R=\{(x,y)\mid a(x)\le x\le b(x), c\le y\le d\}\), met continue functie \(x=a(y)\) en \(x=b(y)\), dan geldt:\[ \iint_R f(x,y)\,\dd(x,y)=\int_{y=c}^{y=d}\left(\int_{x=a(y)}^{x=b(y)}f(x,y)\,\dd x\right)\dd y\]
- Als \(R\) \(x\)- en \(y\)-eenvoudig is, d.w.z. \[ R=\{(x,y)\mid a(x)\le x\le b(x), c\le y\le d\}\quad\text{en}\quad R=\{(x,y)\mid a\le x\le b, c(x)\le y\le d(x)\}\] voor zekere continue functies \(x=a(y)\), \(x=b(y)\), \(y=c(x)\) en \(y=d(x)\), dan geldt: \[ \iint_R f(x,y)\,\dd(x,y)=\int_{x=a}^{x=b}\left(\int_{y=c(x)}^{y=d(x)}f(x,y)\,\dd y\right)\dd x=\int_{y=a}^{y=b}\left(\int_{x=a(y)}^{x=b(y)}f(x,y)\,\dd x\right)\dd y\]
\(\iint_R (3x+3y)\,\dd(x,y)={}\)\({{9}\over{10}}\)
De parabolen \(y=x^2\) en \(x=y^2\) snijden elkaar in de oorsprong en in het punt \((1,1)\). Als we het integratiegebied beschouwen als een \(y\)-eenvoudig gebied, dan houden we eerst \(x\) vast (met \(0\le x\le 1\) en integreren voor deze vaste \(x\) naar \(y\). De integratiegrenzen zijn dan \(a(y)=x^2\) en \(b(y)=\sqrt{x}\); zie onderstaande figuur.
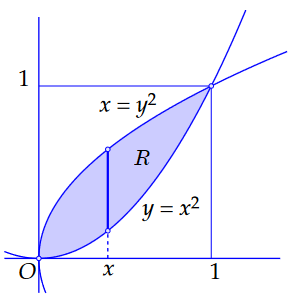
De herhaalde integraal wordt: \[\begin{aligned}\iint_R (3 x+3 y)\,\dd(x,y) &= \int_{x=0}^{x=1}\left(\int_{y=x^2}^{y=\sqrt{x}}(3 x+3 y)\,\dd y\right)\dd x\\[0.25cm] &= \int_{x=0}^{x=1}\biggl[(3 xy+{{3}\over{2}} y^2)\biggr]_{y=x^2}^{y=\sqrt{x}}\,\dd x\\[0.25cm] &= \int_{x=0}^{x=1}\bigl((3 x^{\frac{3}{2}}+{{3}\over{2}} x)-(3 x^3+{{3}\over{2}} x^4)\bigr)\,\dd x\\[0.25cm] &=\biggl[{{6}\over{5}} x^{\frac{5}{2}}+{{3}\over{4}}x^2-{{3}\over{4}} x^4-{{3}\over{10}} x^5\biggr]_{x=0}^{x=1}\\[0.25cm] &= {{6}\over{5}}+{{3}\over{4}}-{{3}\over{4}}-{{3}\over{10}}\\[0.25cm]&={{9}\over{10}} \end{aligned}\]
We kunnen het integratiegebied ook als \(x\)-eenvoudig beschouwen. Dan houden we eerst \(y\) vast (met \(0\le y\le 1\) en integreren voor deze vaste \(y\) naar \(x\). De integratiegrenzen zijn dan \(c(x)=y^2\) en \(d(x)=\sqrt{y}\); zie onderstaande figuur.
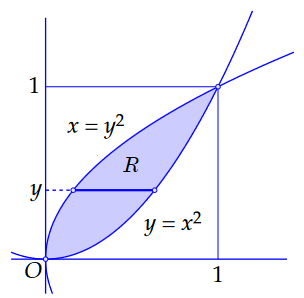
De herhaalde integraal wordt: \[\begin{aligned}\iint_R (3 x+3 y)\,\dd(x,y) &= \int_{y=0}^{y=1}\left(\int_{x=y^2}^{x=\sqrt{y}}(3x+3y)\,\dd x\right)\dd y\\[0.25cm] &= \int_{y=0}^{y=1}\biggl[({{3}\over{2}} x^2+3 xy)\biggr]_{x=y^2}^{x=\sqrt{y}}\,\dd x\\[0.25cm] &= \int_{y=0}^{y=1}\bigl(({{3}\over{2}} y+3 y^{\frac{3}{2}})-({{3}\over{2}} y^4+3 y^3)\bigr)\,\dd x\\[0.25cm] &=\biggl[{{3}\over{4}} y^2+{{6}\over{5}} y^{\frac{5}{2}}-{{3}\over{10}} y^5-{{3}\over{4}} y^4\biggr]_{y=0}^{y=1}\\[0.25cm] &= {{3}\over{4}}+{{6}\over{5}}-{{3}\over{10}}-{{3}\over{4}}\\[0.25cm]&={{9}\over{10}} \end{aligned}\]
De route is anders, maar het resultaat is hetzelfde.
Aanpak voor het berekenen van een dubbelintegraal Bij de exacte berekening van een dubbelintegraal \(\iint_R f(x,y)\dd(x,y)\) over een niet-rechthoekig gebied \(R\) kun je als volgt te werk gaan.
- Maak een schets van het gebied \(R\) in het \(xy\)-vlak.
- Ga na of het integratiegebied \(x\)-eenvoudig is, \(y\)-eenvoudig is, of misschien wel allebei.
- Beslis aan de hand van de integrand en de aard van het integratiegebied of je eerst naar \(x\) of \(y\) gaat integreren.
Bij integratie eerst naar \(y\) (d.w.z. \(R\) is \(y\)-eenvoudig):
- Bepaal de linkergrens \(a\) en rechtergrens \(b\) voor \(x\) als uitersten van \(R\) in de horizontale richting.
- Trek een verticale hulplijn op positie \(x\) tussen \(a\) en \(b\) in de schets van \(R\)
- Bepaal de ondergrens \(c(x)\) en de bovengrens \(d(x)\) voor het lijnstuk dat binnen \(R\) blijft op horizontale positie \(x\)
- Bereken \(\displaystyle \int_{y=c(x)}^{y=d(x)}\,f(x,y)\,\dd y\). Dit is een functie van \(x\).
- Integreer laatstgenoemde functie met integratiegrenzen \(a\) en \(b\). Dus: \[\iint_R f(x,y)\,\dd(x,y)=\int_{x=a}^{x=b}\left(\int_{y=c(x)}^{y=d(x)}f(x,y)\,\dd y\right)\dd x\]
Bij integratie eerst naar \(x\) (d.w.z. \(R\) is \(x\)-eenvoudig):
- Bepaal de ondergrens \(c\) en bovengrens \(d\) voor \(y\) als uitersten van \(R\) in de verticale richting.
- Trek een horizontale hulplijn op positie \(y\) tussen \(c\) en \(d\) in de schets van \(R\)
- Bepaal de linkergrens \(a(y)\) en de rechtergrens \(b(y)\) voor het lijnstuk dat binnen \(R\) blijft op verticale positie \(y\)
- Bereken \(\displaystyle \int_{x=a(y)}^{x=d(y)} f(x,y)\,\dd x\). Dit is een functie van \(y\).
- Integreer laatstgenoemde functie met integratiegrenzen \(c\) en \(d\). Dus: \[\iint_R f(x,y)\, \dd(x,y)=\int_{y=c}^{y=d}\left(\int_{x=a(y)}^{x=b(y)} f(x,y)\,\dd x\right)\dd y\]
