Meervoudige integralen: Dubbelintegralen
Verandering van variabelen in dubbelintegralen
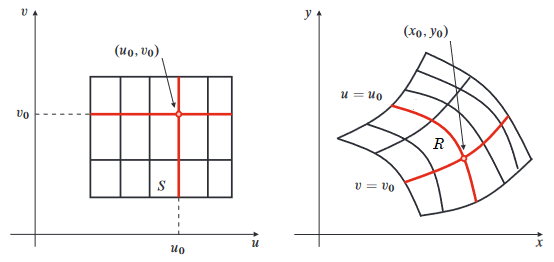
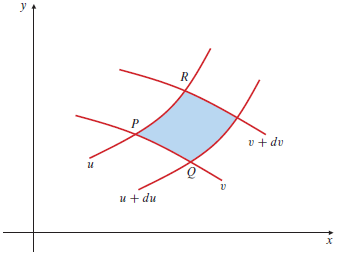
Dubbelintegraal in andere coördinaten Stel dat \(x=x(u,v)\) en \(y=y(u,v)\) een inverteerbare afbeelding van een gebied \(S\) in het \(uv\)-vlak is naar een gebied \(R\) in het \(xy\)-vlak en stel dat de functies \(x\) en \(y\) continue afgeleides hebben op \(S\). Als de dubbelintegraal \(\displaystyle \iint_R f(x,y)\,\dd(x,y)\) bestaat (oftewel \(f(x,y)\) integreerbaar is op\(R\)) en als \(g(u,v)=f\bigl(x(u,v), y(u,v)\bigr)\), dan is \(g(u,v)\) integreerbaar op \(S\) en \[\iint_R f(x,y)\,\dd(x,y) =\iint_S g(u,v)\cdot \bigl|J(u,v)\bigr|\,\dd u\, \dd v)\] waaarbij de Jacobiaan \(J(u,v)\) gedefinieerd is als \[\begin{aligned}J(u,v)&=\det\matrix{\dfrac{\partial x}{\partial u} &\dfrac{\partial x}{\partial v}\\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v}}\\[0.25cm] &= \frac{\partial x}{\partial u} \cdot \frac{\partial y}{\partial v} -\frac{\partial x}{\partial v} \cdot \frac{\partial y}{\partial u}\end{aligned} \]
Bewijsschets Met de coördinatentransformatie \((u,v)\mapsto \bigl(x(u,v), y(u,v)\bigr)\) wordt een rechthoekig gebied in het \(uv\)-vlak, laten we het \(S\) noemen, afgebeeld op een niet-noodzakelijk rechthoekig gebied in het \(xy\)-vlak, laten we dit \(R\) noemen. Om de dubbelintegraal van een functie op \(S\) te berekenen overdekken we \(S\) met een rechthoekige verdeling met maaswijdtes \(\dd u\) en \(\dd v\). Kies een vast hoekpunt \((u_0,v_0)\) in een deelrechthoekje van de verdeling. De hoekpunten \(P=(u_0,v_0)\), \(Q=(u_0+\dd u, v_0)\) en \(R=(u_0, v_0+\dd v)\) worden respectievelijk afgebeeld op \(\bigl(x_0,y_0\bigr)=\bigl(x(u_0, v_0), y(u_0, v_0)\bigr)\) \(\bigl(x(u_0+\dd u, v_0), y(u_0+\dd u, v_0)\bigr)\) en \(\bigl(x(u_0,v_0+\dd u), y(v_0,u_0+\dd u)\bigr)\). De transformatie wordt hieronder gevisualiseerd.
Bij benadering wordt het deelrechthoekje in het \(uv\)-vlak afgebeeld op een ruitje met twee kanten gegeven door de vectoren \(\vec{PQ}\) en \(\vec{PR}\). In onderstaande figuur laten we nog zien dat het een benadering is, maar in het infinitesimale geval is het wel juist.
Er geldt in het infinitesimale geval: \[\vec{PQ}=\cv{\dfrac{\partial x}{\partial u} \\ \dfrac{\partial y}{\partial u}}\cdot \dd u\qquad\text{en} \qquad \vec{PR}=\cv{\dfrac{\partial x}{\partial v} \\ \dfrac{\partial y}{\partial v}}\cdot \dd v\] De oppervlakte van het ruitje is de lengte van het uitproduct van de vectoren \(\vec{PQ}\) en \(\vec{PR}\). Dit is gelijk aan \(\bigl|J(u,v)\bigr|\,\dd u\,\dd v\).
We weten nu hoe een rechthoekig deelgebiedje wordt getransformeerd wordt. Hierna moeten we nog een sommatie over de verdeling doen en een limiet nemen om het bewijs rond te krijgen.
Door de substitutie \[u=x+y\quad\text{en}\quad v=x-y\] wordt de integrand een eenvoudigere uitdrukking, namelijk \(e^{\frac{v}{u}}\). Het integratiegebied wordt afgebeeld op een nieuwe driehoek \(S\) in het \(uv\)-vlak begrens door de lijnen \(u=v\), \(u=-v\) en \(u=1\). We kunnen immers \(x\) en \(y\) isoleren in de bovenstaande vergelijkingen als \[x=\frac{1}{2}(u+v)\quad\text{en}\quad y=\frac{1}{2}(u-v)\] Daardoor: \[\begin{aligned} y=-x+1&\iff u=1\\[0.25cm] x=0 &\iff u=-v\\[0.25cm] y=0 &\iff u=v\end{aligned}\] Hiermee hebben we dan de coördinatentransformatie die \(S\) afbeeldt op \(R\) in het \(xy\)-vlak. De Jacobiaan \(J(u,v)\) is ook direct te berekenen: \[\begin{aligned}J(u,v) &= \det\matrix{\frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & -\frac{1}{2}}\\[0.25cm] &= -\frac{1}{2}\end{aligned}\] De berekening van de dubbelintegraal verloopt nu als volgt: \[\begin{aligned} \iint_R e^{\frac{x-y}{x+y}}\,\dd(x,y) &= \iint_S e^{\frac{v}{u}}\,\bigl|J(u,v)\bigr|\,\dd(u,v) \\[0.25cm] &= \frac{1}{2}\int_{u=0}^{u=1}\left(\int_{v=-u}^{v=u}e^{\frac{v}{u}}\,\dd v\right)\dd u\\[0.25cm] &= \frac{1}{2}\int_{u=0}^{u=1} \biggl[u\,e^{\frac{v}{u}}\biggr]_{v=-u}^{v=u}\;\dd u\\[0.25cm] &=\frac{1}{2}\int_{u=0}^{u=1}\left(e-\frac{1}{e}\right)u\,\dd u\\[0.25cm] &= \frac{1}{2}\left(e-\frac{1}{e}\right)\cdot\biggl[\frac{1}{2}u^2\biggr]_{u=0}^{u=1}\\[0.25cm] &= \frac{1}{4}\left(e-\frac{1}{e}\right)\end{aligned}\]
