Multiple integrals: Triple integrals
Change of variables in triple integrals: spherical and cylindrical coordinates
Triple integral in other coordinates Suppose \(x=x(u,v,w)\), \(y=y(u,v,w)\) and \(z=z(u,v,w)\) is an invertible mapping from a bounded region \(S\) in the \(uvw\)-plane to a region \(R\) in the \(xyz\) plane and suppose the functions \(x\), \(y\) and \(z\) have continuous derivatives on \(S\). If the triple integral \(\displaystyle \iint_R f(x,y,z)\,\dd(x,y,z)\) exists (i.e. \(f(x,y,z)\) is integrable on \(R\) ) and if \(g(u,v,w)=f\bigl(x(u,v,w), y(u,v,w), z(u,v,w)\bigr)\), then \(g(u,v,w)\) is integrable on \(S\) and \[\iint_R f(x,y,z)\,\dd(x,y,z) =\iint_S g(u,v,w)\cdot \bigl|J(u,v,w)\bigr|\,\dd u\,\dd v\,\dd w\] with the Jacobian \(J(u,v,w)\) defined as \[\begin{aligned}J(u,v,w) &=\det\matrix{\dfrac{\partial x}{\partial u} &\dfrac{\partial x}{\partial v} &\dfrac{\partial x}{\partial w}\\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w}\\ \dfrac{\partial z}{\partial u} & \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w}}\\[0.25cm] &= \dfrac{\partial x}{\partial u}\cdot \det\matrix{\dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w}\\ \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w}} - \dfrac{\partial y}{\partial u}\cdot \det\matrix{\dfrac{\partial x}{\partial v} & \dfrac{\partial x}{\partial w}\\ \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w}}+\dfrac{\partial z}{\partial u}\cdot \det\matrix{\dfrac{\partial x}{\partial v} & \dfrac{\partial x}{\partial w}\\ \dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w}} \\[0.25cm] &\phantom{abcuva}\blue{\text{expansion of the determinant along the first column}} \end{aligned} \]
Example of scaling Suppose you want to calculate the volume \(V\) of an ellipsoid \[E=\{(x,y,x)\mid \frac{x^2}{a^2}+ \frac{y^2}{b^2}+ \frac{z^2}{c^2}\le 1]\] with \(a>0, b>0, c>0\). Under the transformation \(x=a\,u, y=b\,v, z=c\,w\) the unit sphere \[R=\{(u,v,w)\mid u^2+v^2+w^2\le 1\}\] is mapped onto the ellipsoid \(E\). The Jacobian \(J(u,v,w)\) can easily be calculated: \[\begin{aligned}J(u,v,w) &=\det\matrix{a & 0 & 0\\ 0 & b & 0 \\ 0 & 0 & c}\\[0.25cm] &= a\,b\,c\end{aligned}\] The volume \(V\) of an ellipsoid can now be calculated as follows: \[\begin{aligned} V &= \iiint_E \dd(x,y,z)\\[0.25cm] &= \iiint_{R} a\,b\,c\,\dd u\,\dd v\,\dd w\\[0.25cm] &= a\,b\,c\cdot \mathrm{volume of }(R)\\[0.25cm] &= \frac{4}{3}\pi\,a\,b\,c\end{aligned}\]
Integrals in cylindrical coordinates Cylindrical coordinates are actually polar coordinates \(x=r\cos\varphi\) and \(y=r\sin\varphi\) with an extra dimension \(z\). As with polar coordinates, \(\bigl|J(r,\varphi,z\bigr|=r\) and therefore \[\iiint_R f(x,y,z)\dd(x,y,z)=\iiint_Sf(r\cos\varphi, r\sin\varphi,z)\,r\,\dd r\,\dd\varphi\,\dd z\] apply
First note that the region of integration \(R\) can be described in cylindrical coordinates with the region of integration \[S=\{(r,\varphi,z)\mid 0\le r\le 1,\;\; 0\le \varphi\le 2\pi,\;\; 0\le z\le 2\}\] . The requested triple integral can now be calculated as an iterated integral in the following way: \[\begin{aligned} \iiint_R (x^2+y^2+ z)\,\dd(x,y,z) &= \iiint_S (r^2+ z)\,r\,\dd r\,\dd\varphi\,\dd z \\[0.25cm] &= \int_{z=0}^{z=2}\left(\int_{\varphi=0}^{\varphi=2\pi}\left(\int_{r=0}^{r=1}(r^3+z\,r)\,\dd r\right)\dd \varphi\right)\dd z\\[0.25cm] &= \int_{z=0}^{z=2}\left(\int_{\varphi=0}^{\varphi=2\pi} \biggl[\frac{1}{4}r^4+\frac{1}{2}z\,r^2\biggr]_{r=0}^{r=1}\;\dd\varphi\right)\dd z\\[0.25cm] &= \int_{z=0}^{z=2}\left(\int_{\varphi=0}^{\varphi=2\pi}\Bigl({{1}\over{4}} +{{1}\over{2}}z\Bigr)\,\dd\varphi\right)\dd z \\[0.25cm] &= \int_{z=0}^{z=2}\biggl[\Bigl({{1}\over{4}} +{{1}\over{2}}z\Bigr)\varphi\biggr]_{\varphi=0}^{\varphi=2\pi}\;\dd z\\[0.25cm] &= 2\pi \int_{z=0}^{z=2}\Bigl({{1}\over{4}} +{{1}\over{2}}z\Bigr)\dd z\\[0.25cm] &= \biggl[{{1}\over{4}}z+{{1}\over{2}}\times \frac{1}{2}z^2\biggr]_{z=0}^{z=2}\\[0.25cm] &= \biggl[{{1}\over{4}}z+{{1}\over{4}}z^2\biggr]_{z=0}^{z=2}\\[0.25cm] &={{1}\over{4}}\times 2+{{1}\over{4}}\times 2^2\\[0.25cm] &= {{3}\over{2}}\end{aligned}\]
Integrals in spherical coordinates Spherical coordinates \((r,\varphi,\theta)\) are defined as in the figure below, with the following formulas \[\begin{aligned}x(r,\varphi,\theta)&=r\cos\varphi\sin\theta\\ y(r,\varphi,\theta)&=r\sin\varphi\sin\theta\\ z(r,\varphi,\theta) &= r\cos\theta\end{aligned}\]
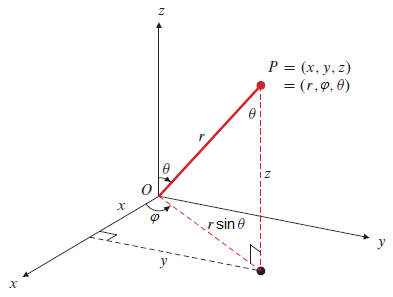
In this case the Jaconian of the coordinate transformation is \(\bigl|J(r,\varphi,z\bigr|=r^2\cos\theta\) and therefore \[\iiint_R f(x,y,z)\dd(x,y,z)=\iiint_S f(r\cos\varphi\cos\theta, r\sin\varphi\cos\theta,r\sin\theta)\,r^2\sin\theta\,\dd r\,\dd\varphi\,\dd\theta\]
First note that the region of integration \(R\) can be described in spherical coordinates with the region of integration \[S=\{(r,\varphi,\theta)\mid 0\le r\le 1,\;\; 0\le \varphi\le 2\pi,\;\; 0\le \theta \le \pi\}\] The requested triple integral can now be calculated as iterated integral in the following way:
\[\begin{aligned} \iiint_R \sqrt{x^2+y^2+z^2}\,\dd(x,y,z) &=\int_{\theta=0}^{\theta=\pi}\left(\int_{\varphi=0}^{\varphi=2\pi}\left(\int_{r=0}^{r=1}r\cdot r^2\sin\theta\,\dd r\right)\dd\varphi\right)\dd \theta\\[0.25cm] &=\int_{\theta=0}^{\theta=\pi}\left(\int_{\varphi=0}^{\varphi=2\pi}\left(\int_{r=0}^{r=1}r^3\sin\theta\,\dd r\right)\dd\varphi\right)\dd \theta\\[0.25cm] &=\int_{\theta=0}^{\theta=\pi}\left(\int_{\varphi=0}^{\varphi=2\pi}\biggl[\frac{1}{4}r^4\sin\theta\biggr]_{r=0}^{r=1}\;\dd\varphi\right)\dd \theta\\[0.25cm] &=\int_{\theta=0}^{\theta=\pi}\left(\int_{\varphi=0}^{\varphi=2\pi}\frac{1}{4}\sin\theta\,\dd\varphi\right)\dd \theta\\[0.25cm] &=\int_{\theta=0}^{\theta=\pi}2\pi\cdot\frac{1}{4}\sin\theta\,\dd \theta\\[0.25cm] &=\biggl[-\frac{1}{2}\pi\cos\theta\biggr]_{\theta=0}^{\theta=\pi}\\[0.25cm]&= \pi \end{aligned}\]
