Meervoudige integralen: Drievoudige integralen
Verandering van variabelen in drievoudige integralen: bol- en cilindercoördinaten
Drievoudige integraal in andere coördinaten Stel dat \(x=x(u,v,w)\), \(y=y(u,v,w)\) en \(z=z(u,v,w)\) een inverteerbare afbeelding van een begrensd gebied \(S\) het \(uvw\)-vlak is naar een gebied \(R\) in het \(xyz\)-vlak en stel dat de functies \(x\), \(y\) en \(z\) continue afgeleides hebben op \(S\). Als de drievoudige integraal \(\displaystyle \iint_R f(x,y,z)\,\dd(x,y,z)\) bestaat (oftewel \(f(x,y,z)\) integreerbaar is op\(R\)) en als \(g(u,v,w)=f\bigl(x(u,v,w), y(u,v,w), z(u,v,w)\bigr)\), dan is \(g(u,v,w)\) integreerbaar op \(S\) en \[\iint_R f(x,y,z)\,\dd(x,y,z) =\iint_S g(u,v,w)\cdot \bigl|J(u,v,w)\bigr|\,\dd u\,\dd v\,\dd w\] waaarbij de Jacobiaan \(J(u,v,w)\) gedefinieerd is als \[\begin{aligned}J(u,v,w) &=\det\matrix{\dfrac{\partial x}{\partial u} &\dfrac{\partial x}{\partial v} &\dfrac{\partial x}{\partial w}\\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w}\\ \dfrac{\partial z}{\partial u} & \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w}}\\[0.25cm] &= \dfrac{\partial x}{\partial u}\cdot \det\matrix{\dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w}\\ \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w}} - \dfrac{\partial y}{\partial u}\cdot \det\matrix{\dfrac{\partial x}{\partial v} & \dfrac{\partial x}{\partial w}\\ \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w}}+\dfrac{\partial z}{\partial u}\cdot \det\matrix{\dfrac{\partial x}{\partial v} & \dfrac{\partial x}{\partial w}\\ \dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w}} \\[0.25cm] &\phantom{abcuva}\blue{\text{ontwikkeling van de determinant langs de eerste kolom}} \end{aligned} \]
Voorbeeld van schaling Stel dat je de inhoud \(I\) van een ellipsoïde \[E=\{(x,y,x)\mid \frac{x^2}{a^2}+ \frac{y^2}{b^2}+ \frac{z^2}{c^2}\le 1]\] met \(a>0, b>0, c>0\) wilt berekenen. Onder de transformatie \(x=a\,u, y=b\,v, z=c\,w\) wordt de eenheidsbol \[R=\{(u,v,w)\mid u^2+v^2+w^2\le 1\}\] afgebeeld op de ellipsoïde \(E\). De Jacobiaan \(J(u,v,w)\) is eenvoudig te berekenen: \[\begin{aligned}J(u,v,w) &=\det\matrix{a & 0 & 0\\ 0 & b & 0 \\ 0 & 0 & c}\\[0.25cm] &= a\,b\,c\end{aligned}\] De inhoud \(I\) van een ellipsoïde is nu als volgt te berekenen: \[\begin{aligned} I &= \iiint_E \dd(x,y,z)\\[0.25cm] &= \iiint_{R} a\,b\,c\,\dd u\,\dd v\,\dd w\\[0.25cm] &= a\,b\,c\cdot \mathrm{inhoud}(R)\\[0.25cm] &= \frac{4}{3}\pi\,a\,b\,c\end{aligned}\]
Integralen in cilindercoördinaten Cilindercoördinaten zijn eigenlijk poolcoördinaten \(x=r\cos\varphi\) en \(y=r\sin\varphi\) met een extra dimensie \(z\). Net als bij poolcoördinaten geldt dan \(\bigl|J(r,\varphi,z\bigr|=r\) en dus \[\iiint_R f(x,y,z)\dd(x,y,z)=\iiint_Sf(r\cos\varphi, r\sin\varphi,z)\,r\,\dd r\,\dd\varphi\,\dd z\]
Merk eerst op dat het integratiegebied \(R\) in cilindercoördinaten beschreven kan worden met als integratiegebied \[S=\{(r,\varphi,z)\mid 0\le r\le 2,\;\; 0\le \varphi\le 2\pi,\;\; 0\le z\le 3\}\] De gevraagde drievoudige integraal kan nu als volgt berekend worden als herhaalde integraal: \[\begin{aligned} \iiint_R (x^2+y^2+ z^2)\,\dd(x,y,z) &= \iiint_S (r^2+ z^2)\,r\,\dd r\,\dd\varphi\,\dd z \\[0.25cm] &= \int_{z=0}^{z=3}\left(\int_{\varphi=0}^{\varphi=2\pi}\left(\int_{r=0}^{r=2}(r^3+z^2\,r)\,\dd r\right)\dd \varphi\right)\dd z\\[0.25cm] &= \int_{z=0}^{z=3}\left(\int_{\varphi=0}^{\varphi=2\pi} \biggl[\frac{1}{4}r^4+\frac{1}{2}z^2\,r^2\biggr]_{r=0}^{r=2}\;\dd\varphi\right)\dd z\\[0.25cm] &= \int_{z=0}^{z=3}\left(\int_{\varphi=0}^{\varphi=2\pi}\Bigl(4 +2z^2\Bigr)\,\dd\varphi\right)\dd z \\[0.25cm] &= \int_{z=0}^{z=3}\biggl[\Bigl(4 +2z^2\Bigr)\varphi\biggr]_{\varphi=0}^{\varphi=2\pi}\;\dd z\\[0.25cm] &= 2\pi \int_{z=0}^{z=3}\Bigl(4 +2z^2\Bigr)\dd z\\[0.25cm] &= \biggl[4z+2\times \frac{1}{3}z^3\biggr]_{z=0}^{z=3}\\[0.25cm] &= \biggl[4z+{{2}\over{3}}z^3\biggr]_{z=0}^{z=3}\\[0.25cm] &=4\times 3+{{2}\over{3}}\times 3^3\\[0.25cm] &= 30\end{aligned}\]
Integralen in bolcoördinaten Bolcoördinaten \((r,\varphi,\theta)\) zijn gedefineerd als in onderstaande figuur, met de volgende formules\[\begin{aligned}x(r,\varphi,\theta)&=r\cos\varphi\sin\theta\\ y(r,\varphi,\theta)&=r\sin\varphi\sin\theta\\ z(r,\varphi,\theta) &= r\cos\theta\end{aligned}\]
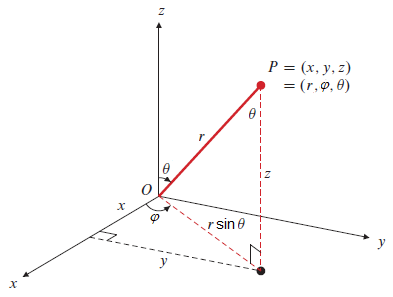
In dit geval is de Jacobiaan van de coördinatentransformatie \(\bigl|J(r,\varphi,z\bigr|=r^2\cos\theta\) en dus \[\iiint_R f(x,y,z)\dd(x,y,z)=\iiint_S f(r\cos\varphi\cos\theta, r\sin\varphi\cos\theta,r\sin\theta)\,r^2\sin\theta\,\dd r\,\dd\varphi\,\dd\theta\]
Merk eerst op dat het integratiegebied \(R\) in bolcoördinaten beschreven kan worden met als integratiegebied \[S=\{(r,\varphi,\theta)\mid 0\le r\le 1,\;\; 0\le \varphi\le 2\pi,\;\; 0\le \theta \le \pi\}\] De gevraagde drievoudige integraal kan nu als volgt berekend worden als herhaalde integraal:
\[\begin{aligned} \iiint_R (x^2+y^2+z^2)\,\dd(x,y,z) &=\int_{\theta=0}^{\theta=\pi}\left(\int_{\varphi=0}^{\varphi=2\pi}\left(\int_{r=0}^{r=1}r^2\cdot r^2\sin\theta\,\dd r\right)\dd\varphi\right)\dd \theta\\[0.25cm] &=\int_{\theta=0}^{\theta=\pi}\left(\int_{\varphi=0}^{\varphi=2\pi}\left(\int_{r=0}^{r=1}r^4\sin\theta\,\dd r\right)\dd\varphi\right)\dd \theta\\[0.25cm] &=\int_{\theta=0}^{\theta=\pi}\left(\int_{\varphi=0}^{\varphi=2\pi}\biggl[\frac{1}{5}r^5\sin\theta\biggr]_{r=0}^{r=1}\;\dd\varphi\right)\dd \theta\\[0.25cm] &=\int_{\theta=0}^{\theta=\pi}\left(\int_{\varphi=0}^{\varphi=2\pi}\frac{1}{5}\sin\theta\,\dd\varphi\right)\dd \theta\\[0.25cm] &=\int_{\theta=0}^{\theta=\pi}2\pi\cdot\frac{1}{5}\sin\theta\,\dd \theta\\[0.25cm] &=\biggl[-\frac{2}{5}\pi\cos\theta\biggr]_{\theta=0}^{\theta=\pi}\\[0.25cm]&= \frac{4}{5}\pi\end{aligned}\]
