Multiple integrals: Applications of multiple integrals
Calculation of the area of a 2D-region
The area \(A\) of a closed and bounded region \(R\) in two-dimensional space is given by the following formula: \[A=\iint_R\dd(x,y)\]
Calculate the area of the region enclosed by the graphs of the functions \(\cos(x)\) and \(2\cos(x)\) and the vertical axis via a double integral. So determine in this manner the area of the shaded region in the figure below.
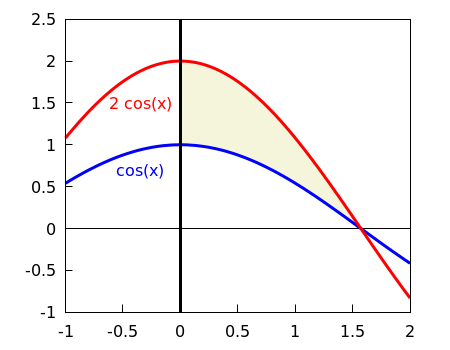
The shaded region, let's call it \(R\), consists of all points \((x,y)\) for which \(0\le x\ \le \tfrac{1}{2}\pi\) and \(\cos(x)\le y\le 2\cos(x)\). The area of the shaded region can then be determined via a double integral in the following way: \[\begin{aligned}\text{area}&=\iint_R \dd(x,y)\\[0.25cm] &= \int_{x=0}^{x=\frac{1}{2}\pi}\left(\int_{y=\cos(x)}^{y=2\cos(x)}\dd y\right)\dd x\\[0.25cm]&= \int_{x=0}^{x=\frac{1}{2}\pi}\bigl(2\cos(x)-\cos(x)\bigr)\,\dd x\\[0.25cm] &=\int_{x=0}^{x=\frac{1}{2}\pi}\cos(x)\,\dd x\\[0.25cm] &=\biggl[\sin(x)\biggr] _{x=0}^{x=\frac{1}{2}\pi}\\[0.25cm] &=\sin(\tfrac{1}{2}\pi)-\sin(0)\\[0.25cm] &= 1-0\\[0.25cm] &= 1 \end{aligned}\] Note that after integration in \(y\) it boils down to the usual determination of the area of a region enclosed by two functions by means of integration of functions of one variable.
Such a calculation of an area can also be performed in polar coordinates when the area is easier to define in these coordinates. We look at two cases.
We consider an region defined in polar coordinates as the region enclosed by two half-lines and a curve defined by \(r=f(\varphi)\) as shown as a shaded region in the diagram below.
The area \(A\) of the shaded region can be calculated in the following way: \[\begin{aligned}O&=\int_{\varphi=\alpha}^{\varphi=\beta}\left(\int_{r=0}^{r=f(\varphi)}\,r\,\dd r\right)\dd\varphi\\[0.25cm] &= \int_{\varphi=\alpha}^{\varphi=\beta}\biggl[\frac{1}{2}r^2\biggr]_{r=0}^{r=f(\varphi)}\;\dd\varphi\\[0.25cm] &= \frac{1}{2}\int_{\varphi=\alpha}^{\varphi=\beta}f(\varphi)^2\,\dd\varphi\end{aligned}\]
We consider a region defined in polar coordinates as the region enclosed by two half-lines and two curves defined by \(r_0=f(\varphi)\) and \(r_1=g(\varphi)\) as shown as a shaded region in the diagram below.
The area \(A\) of the shaded reason can be calculated based on the previous rule in the following way: \[O=\frac{1}{2}\int_{\varphi=\alpha}^{\varphi=\beta}\left(f(\varphi)^2-g(\varphi)^2\right)\,\dd\varphi\]
Calculate the area of the region inside the curve described by \(r = 3 + 2\sin(\varphi)\) and outside the curve \(r = 2\) (see the shaded part of the figure below).
We first calculate the intersection points of \(r = 3 + 2\sin(\varphi)\) and \(r = 2\). Those are given by values of \(\varphi\) satisfying \(2 = 3 + 2\sin(\varphi)\). So \(\sin(\varphi) = -\frac{1}{2}\), so \(\varphi = -\frac{1}{6}\pi\) and \(\varphi = \frac{7}{6}\pi\). The requested region is therefore equal to \[\begin{aligned}
\frac{1}{2}\int_{-\frac{1}{6}\pi}^{\frac{7}{6}\pi}\bigl( (3 + 2 \sin(\varphi))^2 - 2^2\bigr) \, \dd\varphi &=
\frac{1}{2}\int_{-\frac{1}{6}\pi}^{\frac{7}{6}\pi} \bigl( 5 + 12 \sin(\varphi) + 4 \sin(\varphi)^2\bigr) \,\dd\varphi
\\[0.25cm]
&=\frac{1}{2} \int_{-\frac{1}{6}\pi}^{\frac{7}{6}\pi}\bigl( 7 + 12 \sin(\varphi) - 2\cos(2 \varphi)\bigr) \, \dd\varphi
\\[0.25cm]
&= \frac{1}{2}\biggl[ 7 \varphi - 12\cos(\varphi) -\sin(2\varphi) \biggr]_{-\frac{1}{6}\pi}^{\frac{7}{6}\pi}
\\[0.25cm]
&= \frac{14}{3}\pi+\frac{11}{2} \sqrt{3}
\end{aligned}\]
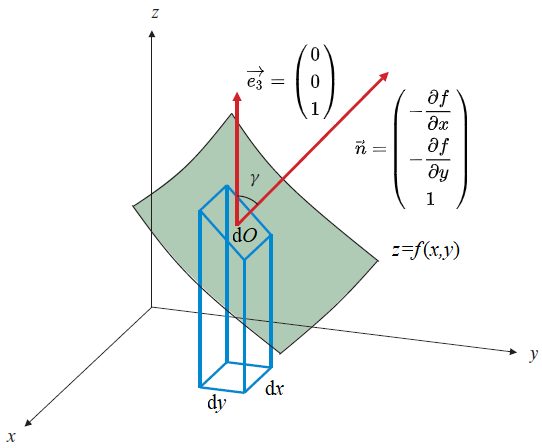
Finally, we look at the area of a surface with equation \(z=f(x,y)\). A calculation rule can also be derived for this sutation.
Suppose \(f\) is a function of two variables \(x\) and \(y\) with continuous partial derivatives and defined on a bounded region \(R\) in the \(xy\)-plane. Then the area \(A\) of the surface \(z=f(x,y)\) in 3-dimensional space above the region \(R\) can be calculated as follows: \[O=\iint_R \sqrt{1+\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2}\,\dd(x,y)\]
In a point \((x,y)\) on \(R\) we can approximate the surface defined by the equation \(z=f(x,y)\) with the tangent plane in the point \((x,y,f(x,y))\). The normal vector \(\vec{n}\) of the tangent plane is given by \[\vec{n}=\cv{-\dfrac{\partial f}{\partial x}\\-\dfrac{\partial f}{\partial y}\\1}\] We can project a surface element \(\dd(x,y)=\dd x\dd y\) vertically onto the tangent plane and then we get the differential \(\dd A\) of the required area \(A\). The area of the projected surface element scales by the factor \(1/\cos(\gamma)\), where \(\gamma\) is the angle between the normal vector \(\vec{n}\) and the unit vector \(\vec{e_3}\) in the \(z\) direction. The situation is sketched in the figure below.
We can calculate the factor \(1/\cos(\gamma)\) using the inner product: \[\begin{aligned}\cos(\gamma)&=\frac{\vec{n}\boldsymbol{\cdot}\vec{e_3}}{\lVert\vec{n}\rVert\cdot \lVert\vec{e_3}\rVert}\\[0.25cm] &= \frac{1}{\sqrt{1+\left(\dfrac{\partial f}{\partial x}\right)^2+\left(\dfrac{\partial f}{\partial y}\right)^2}}\end{aligned}\] So: \[\dd A=\sqrt{1+\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2}\,\dd(x,y)\] or \[A=\iint_R \sqrt{1+\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2}\,\dd(x,y)\]
