Gene regulation: Dynamical system for proteins
 Gene expression with negative feedback
Gene expression with negative feedback
So far we have not really introduced feedback on protein formation; therefore we need a network of genes. The simplest model for negative feedback is represented by the following scheme [cf. Figure 8-76A in Alberts et al. (2015, 6th Edition, p. 515)].
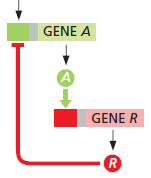
Due to a input signal, the expression of the gene A to the protein A starts. This protein formed is an activating transcription factor for the gene R, which in turn forms a protein R that acts as inhibitory regulator protein for the transcription of gene A.
By using the previous formulas for gene expression, we come to the following set of differential equations for the proteins A and R: \[\begin{aligned}\frac{\dd[\text{A}]}{\dd t}&=\frac{V_\text{A}\cdot K_\text{R}}{K_\text{R}+[\text{R}]}-\frac{[\text{A}]}{\tau_\text{A}}\\ \\ \frac{\dd[\text{R}]}{\dd t}&=\frac{V_\text{R}\cdot [\text{A}]}{K_\text{A}+[\text{A}]}-\frac{[\text{R}]}{\tau_\text{R}}\end{aligned}\]
By scaling we can reduce the system of differential equations to the following system of two quantities \(u\) and \(v\) that are associated with the scaled concentrations of A and R: \[\begin{aligned} \frac{\dd u}{\dd t}&= \frac{\alpha}{1+v}-u\\ \\\frac{\dd v}{\dd t}&= \frac{\beta u}{1+u}-v\end{aligned}\] Scaling is an important part of modelling as a way to get simpler systems with fewer parameters.
Let us for convenience choose \(\alpha=\beta=1\). Then we get: \[\begin{aligned} \frac{\dd u}{\dd t}&= \frac{1}{1+v}-u\\ \\\frac{\dd v}{\dd t}&= \frac{u}{1+u}-v\end{aligned}\] We can determine an equilibrium, in this case even exactly by figuring out where the two derivatives in the differential equation system are simultaneously equal to zero. In the theory of dynamical systems, this is called a singular point.
For an equilibrium \((u,v)\) we should have \[u=\frac{1}{1+v}\quad\text{and}\quad v=\frac{u}{1+u}\] Substitution of the formula for \(v\) in the first equation gives \[u = \frac{1}{1+\dfrac{u}{1+u}}\] or by multiplying the numerator and denominator of the right-hand side with \(u+1\) \[u=\frac{u+1}{2u+1}\] So: \[u(2u+1)=u+1\] Thus: \[2u^2=1\] The only positive solution is \[u=\tfrac{1}{2}\sqrt{2}\] Substitution in the formula for \(v\) and simplification gives \[v=\sqrt{2}-1\] So there is an equilibrium at \[(u,v)=\tfrac{1}{2}\sqrt{2}, \sqrt{2}-1)\]
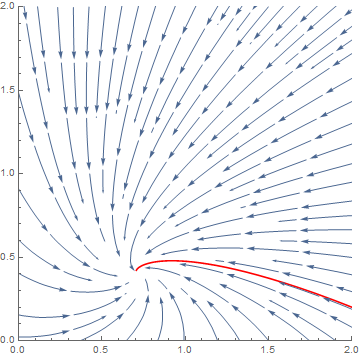
It now turns out that solutions always go in the course of time toward this equilibrium; it is a so-called attracting equilibrium. You see this best in a so-called phase portrait. This is a diagram in which one often draws a number of solution curves at one time and draws the vector field corresponding to the 2-dimensional system of differential equations. At each point \((u,v)\) in the phase portrait we can namely calculate a vector \(\cv{u'\\v'}\) and draw the vector in the plane. In our example, the phase portrait with one red solution curve that starts in \((u,v)=(2, 0.2)\) looks as follows: