Gene regulation: Dynamical system for proteins
 Gene regulation of oscillations
Gene regulation of oscillations
A closed chain of genes, of which each protein that is formed acts as inhibitory regulatory protein for the expression of the nextgene in the chain, may lead to oscillations in protein concentrations. As an example, we consider the following scheme [cf. Figure 8-82C in Alberts et al. (2015, 6th Edition, p. 517)] with five inhibitory regulatory proteins V, W, X, Y and Z.
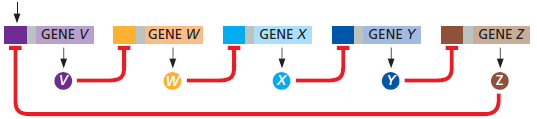
By an input signal the expression of the gene V to the protein V starts. This resulting protein is an inhibitory transcription factor for the gene W, which in turn forms a protein W that acts as an inhibitory regulatory protein for the transcription of gene X, and so on.
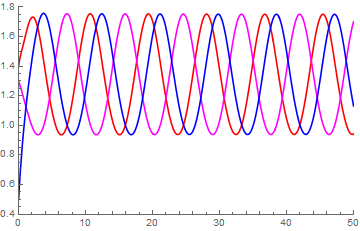
In the example we assume that for each gene, two regulatory proteins can bind to the promoter of the gene. By using the previous formulas for gene expression and by scaling quantities we can reduce the system of differential equations to the following system for five variables \(v, w, x, y,\) and \(z\) corresponding with the scaled concentrations of V, W, X, Y and Z: \[\begin{aligned} \frac{\dd v}{\dd t}&= \frac{\alpha}{1+z^2}-v\\ \\ \frac{\dd w}{\dd t}&= \frac{\beta}{1+v^2}-w\\ \\ \frac{\dd x}{\dd t}&= \frac{\gamma}{1+w^2}-x \\ \\ \frac{\dd y}{\dd t}&= \frac{\delta}{1+x^2}-y \\ \\ \frac{\dd z}{\dd t}&= \frac{\epsilon}{1+y^2}-z\end{aligned}\] We now assume that \[\alpha=\beta=\gamma=\delta=\epsilon=3.5\] and \[v(0)=1.2, w(0)=1, x(0)=1.4, y(0)=1.3, z(0)=0.5\] The system of differential equations can be solved numerically. In the diagram below, the concentration curves of the proteins X, Y, and Z are shown in the colours red, magenta, and blue respectively. You clearly see an oscillating course of the concentrations.
Play with the following simulation to study the behaviour of solutions. It gives the concentration profile of \(x\), \(y\) and \(z\) for the system \[\begin{aligned} \frac{\dd v}{\dd t}&= \frac{\alpha}{1+z^2}-v\\ \\ \frac{\dd w}{\dd t}&= \frac{\alpha}{1+v^2}-w\\ \\ \frac{\dd x}{\dd t}&= \frac{\alpha}{1+w^2}-x \\ \\ \frac{\dd y}{\dd t}&= \frac{\alpha}{1+x^2}-y \\ \\ \frac{\dd z}{\dd t}&= \frac{\alpha}{1+y^2}-z\end{aligned}\] with different initial values and you can also vary \(\alpha\).


