Regulatie van genexpressie: Dynamische systemen voor eiwitten
 Genregulatie met oscillaties
Genregulatie met oscillaties
Een gesloten keten van genen waarvan telkens het eiwit dat door expressie ontstaat als inhiberend regulatoreiwit fungeert voor het opvolgend gen in de keten kan leiden tot oscillatie in eiwitconcentraties. Als voorbeeld bekijken we het onderstaande schema voorgesteld [zie Figuur 8-82C in Alberts et al. (2015, editie 6, p. 517)] met vijf inhibiterende eiwitregulatoren V, W, X, Y en Z.
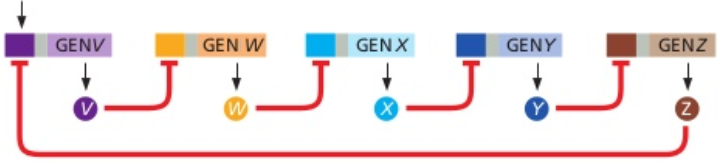
Door een signaal start de expressie van het gen V naar het eiwit V. Dit gevormde eiwit is een inhiberende transcriptiefactor voor het gen W, dat op zijn beurt een eiwit W vormt dat als inhiberend regulatoreiwit fungeert voor de transcriptie van gen X, enzovoorts.
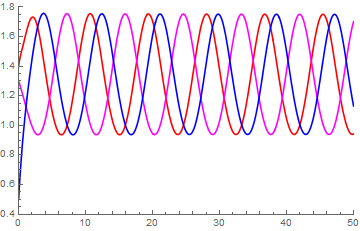
In het voorbeeld dat we gaan bekijken veronderstellen we dat voor elk gen er twee regulatoreiwitten zich kunnen binden met de promotor van het gen. Door de eerdere formules voor genexpressie te gebruiken en door schaling kunnen we het stelsel differentiaalvergelijkingen reduceren tot het volgende stelsel voor vijf grootheden \(v, w, x, y\) en \(z\) die horen bij de geschaalde concentraties van V, W, X, Y en Z: \[\begin{aligned} \frac{\dd v}{\dd t}&= \frac{\alpha}{1+z^2}-v\\ \\ \frac{\dd w}{\dd t}&= \frac{\beta}{1+v^2}-w\\ \\ \frac{\dd x}{\dd t}&= \frac{\gamma}{1+w^2}-x \\ \\ \frac{\dd y}{\dd t}&= \frac{\delta}{1+x^2}-y \\ \\ \frac{\dd z}{\dd t}&= \frac{\epsilon}{1+y^2}-z\end{aligned}\] We nemen nu aan dat \[\alpha=\beta=\gamma=\delta=\epsilon=3.5\] en \[v(0)=1.2, w(0)=1, x(0)=1.4, y(0)=1.3, z(0)=0.5\] Het stelsel van differentiaalvergelijkingen kan numeriek opgelost worden. In onderstaand diagram is het concentratieverloop van de eiwitten X , Y en Z getekend in respectievelijk de kleuren rood, magenta en blauw. Je ziet overduidelijk een oscillerend verloop van de concentraties.
Speel ook eens met onderstaande simulatie om het gedrag van oplossingen te bestuderen. Het geeft het concentratieverloop van \(x\) , \(y\) en \(z\) voor het stelsel \[\begin{aligned} \frac{\dd v}{\dd t}&= \frac{\alpha}{1+z^2}-v\\ \\ \frac{\dd w}{\dd t}&= \frac{\alpha}{1+v^2}-w\\ \\ \frac{\dd x}{\dd t}&= \frac{\alpha}{1+w^2}-x \\ \\ \frac{\dd y}{\dd t}&= \frac{\alpha}{1+x^2}-y \\ \\ \frac{\dd z}{\dd t}&= \frac{\alpha}{1+y^2}-z\end{aligned}\] bij verschillende startwaarden en je kunt ook \(\alpha\) variëren.


