Het opladen van condensatoren die in serie staan verloopt iets anders dan de oplading van een enkele condensator. In onderstaand circuit sluiten we drie condensatoren in serie op elkaar aan en leiden we de formule voor de vervangingscapaciteit in deze situatie af.

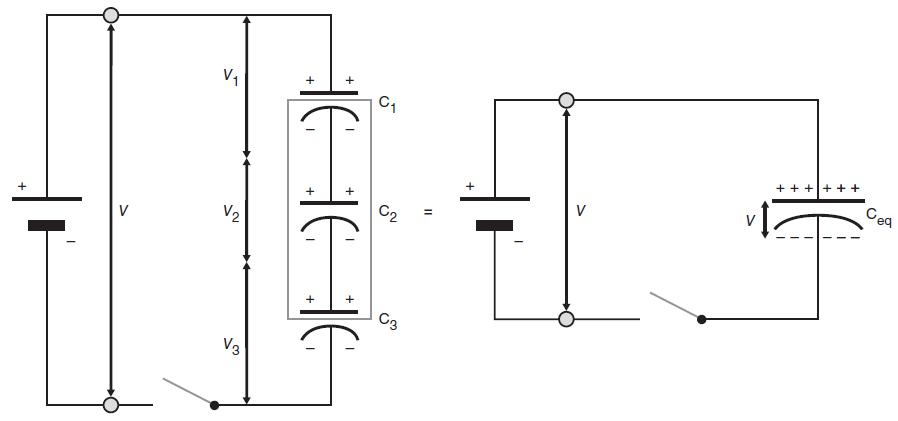
Zodra de schakelaar gesloten wordt stromen elektronen van de bovenste plaat van de eerste condensator met capaciteit $C_1$ naar het plus-aansluiting van de batterij, een positeive ladig achterlatend op de bovenste plaats van de eerste condensator, en tegelijkertijd van de min-aansluiting van de batterij naar de onderste plaat van de derde condensator met capaciteit $C_3$. Er is geen directe verbinding tussen de tweede condensator met capaciteit $C_2$ en de batterij. De stroom van lading tussen de platen van de tweede condensator moet dus geïnduceerd worden door de ladingen op de bovenste plaat van de eerste condensator en de onderste plaat van de derde condensator. De negatieve lading op de onderste plaat van de derde condensator 'stoot' elektronen op de bovenste plaat van de derde condensator af en doet ze stromen naar de onderste plaat van de tweede condensator. Ze laten een positieve lading op de bovenste plaats van de derde condensator achter en leiden tot een negatieve lading op de onderste plaat van de tweede condensator. Evenzo worden elektronen van de bovenste plaat van de tweede condensator afgestoten door de negatieve lading op de onderste plaat van de tweede condensator en dit leidt tot een negatieve lading op de onderste plaat van de eerste condensator en tot een positieve lading op de bovenste plaat van de tweede condensator. Zodra de spanning over de drie condensatoren samen gelijk is aan de bronspanning $V$ die de batterij levert stopt de stroom van elektronen en zijn de condensatoren volledig opgeladen.

Omdat de lading op de condensatorplaten geïnduceerd is moeten ze overal wel aan elkaar gelijk zijn, zeg ter grootte $Q$. Dus:

$$Q=Q_1=Q_2=Q_3$$ Als de lading gelijk blijft, maar het condensator oppervlak waarover het verdeel wordt groter wordt, zal de spanning over het geheel afnemen. Bij een serieschakeling van condensatoren vertegenwoordigt elke condensator een extra oppervlak om dezelfde lading over te verdelen. Dientengevolge is een daling van de potentiaal per condensator van boven naar beneden in het circuit . De som van de spanning over de drie condensatoren is gelijk aan de bronspanning geleverd door de batterij. In formulevorm: $$V=V_1+V_2+V_3$$ De algemene relatie tussen lading $Q$ en spanning $V$ voor een condensator met capaciteit $C$ is $Q=C\cdot V$ en dit geeft bij substitutie de volgende vergelijking: $$\frac{Q}{C}=\frac{Q_1}{C_1}+\frac{Q_2}{C_2}+\frac{Q_3}{C_3}$$ Omdat $Q=Q_1=Q_2=Q_3$ geldt bij deling door $Q$: $$\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}$$ De drie condensatoren in serie kunnen dus vervangen worden door één condensator met capaciteit $C$ of $C_{\mathrm{eq}}$ gegeven door $$\frac{1}{C_{\mathrm{eq}}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}$$ In bovenstaande figuur is de equivalente condensator, ook wel vervangingscondensator genoemd, gevisualiseerd met een groter oppervlak voor opslag van lading (een breder lijnstuk).

Ter illustratie leiden we de formule voor de vervangingscapaciteit van drie parallel geschakelde condensatoren af.

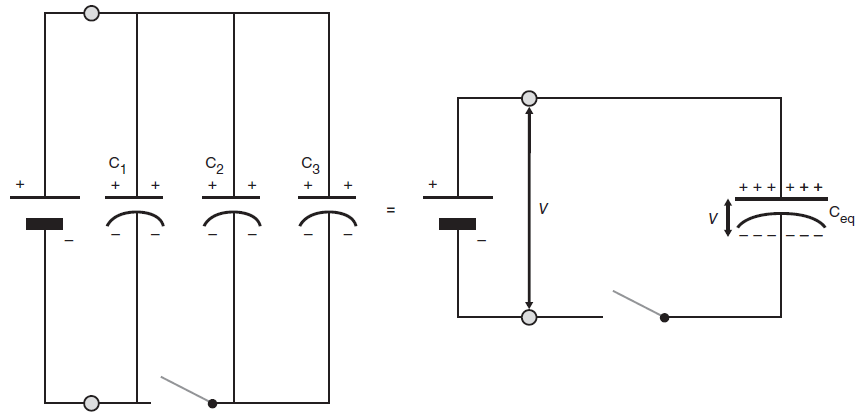
Condensatoren die parallel geschakeld zijn en verbonden zijn met geleidende draad met de uiteinden van een batterij, zoals in onderstaand diagram, slaan samen de lading $Q$ op die de batterij levert. Er geldt dus

$$Q=Q_1+Q_2+Q_3$$ Het potentiaalverschil over elke condensator is gelijk aan de bronspanning geleverd door de batterij: $$V=V_1=V_2=V_3$$ De algemene relatie tussen lading $Q$ en spanning $V$ voor een condensator met capaciteit $C$ geeft nu bij substitutie $$CV=C_1V_1+C_2V_2+C_3V_3$$ en bij deling door $V=V_1=V_2=V_3$ krijgen we dan $$C_{\mathrm{eq}}=C_1+C_2+C_3$$ De vervangingscondensator voor de drie condensatoren heeft dus een capaciteit gelijk aan de som van de capaciteiten van de drie componenten.