Bioelectricity: Core principles
 Resistor
Resistor
Suppose you have the poles of a battery that supplies a voltage source \(V\) connected via a resistor, i.e., via a component that inhibits electric current. In the following drawing of the circuit we have used the rectangular format of the International Electrotechnical Commission (IEC). The US IEEE format, which may encounter in textbooks and which we sometimes use in this course material in borrowed images is ![]() .
.
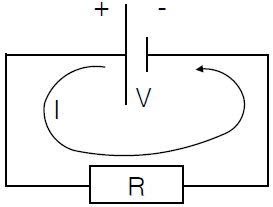
Ohm's law Ohm's law states that the strength of the electric current \(I\), that is to say the amount of charge that passes through the resistor per unit of time, is proportional to the source voltage \(V\), with a constant of proportionality equal to the conductivity \(g\) of the resistor. The conductivity is the reciprocal value of the resistance \(R\) (letter comes from the Latin word "resistere") and is used in biophysics preferably used. The formula we have: \[\begin{aligned} I &=\frac{V}{R}=g\cdot V\\ \\ g &= \frac{1}{R}\end{aligned}\] The unit of resistance is ohm, symbolized by \(\mathbf{\Omega}\); as a unit of conductivity is often used mho, symbolized \(\mathbf{\mho}\), but the SI unit is siemens (\(\mathbf{S}\)). For example, a resistance of 2 ohm is equal to a conductivity of 0.5 siemens.
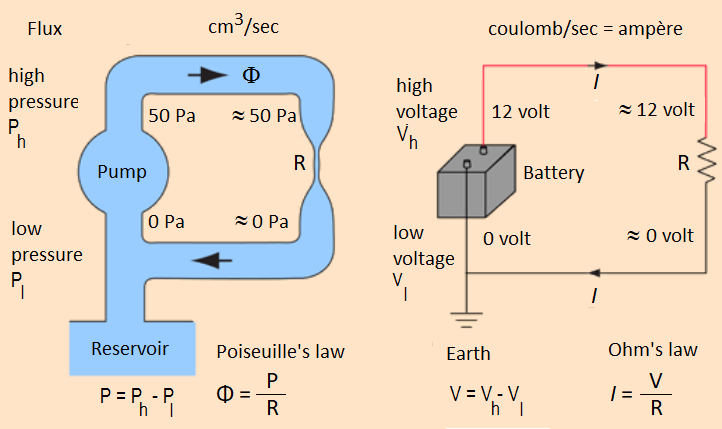
There is a strong analogy between electric current through a resistor and laminar flow of a viscous (that is, viscous) liquid through a tube wherein all particles move in the same direction. A resistor may be considered in this context as a narrowing of the tube at a certain location in the circuit, but a viscous liquid has in fact always along a wall in a tube some resistance (just as an electric wire creates some resistance, but there are also special electrical components with a larger resistance). Under the strength of liquid flow, also called flux and denoted by the Greek letter \(\Phi\), we mean the volume of fluid per unit of time that passes a cross-section of the tube.
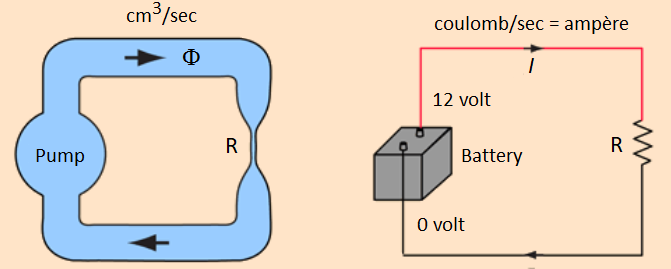
The analogue of Ohm's law is Poiseuille's law, which states that the flux \(\Phi\) is proportional to the pressure difference \(P\) between the ends of the tube, with a proportionality constant equal to the reciprocal value of the flow resistance \(R\). This flow resistance is proportional to the length \(l\) of the tube and the viscosity (viscosity, \(\eta\) ) of the liquid (the larger the mutual adhesion of particles, the more they interfere with each other in their forward movement), and inversely proportional to the fourth power of the radius \(r\) of the tube (the narrower the tube, the greater the resistance). We have the following formula: \[\begin{aligned} \Phi &=\frac{P}{R}\\ \\ R &= \frac{8\,\eta\, l}{\pi\, r^4}\end{aligned}\] A pump is in this context the analogue of a battery or other power source.
The figure below shows the analogy between laminar flow of liquid and electric current extended with a reservoir and earth. The role of a reservoir is the same as an earth in an electrical circuit. Once the pipe system is filled with liquid, the pump may circulate the liquid without the need of the reservoir. The reservoir allows for only a reference pressure. The main function of the earth in an electrical circuit is to make the voltage at a point connected to the earth equal to the reference potential. Usually, the value of 0 volts is assigned.