Bioelektriciteit: Basisbegrippen
 Weerstanden in serie- en parallelschakeling
Weerstanden in serie- en parallelschakeling
Stel dat je twee weerstanden \(R_1\) en \(R_2\) schakelt in een elektrisch cicuit, dan mag je ze bij serie- en parallelschakeling vervangen door één vervangingsweerstand \(R_\mathrm{eq}\) gegeven door een van onderstaande relaties.
Vervangingsweerstand bij serieschakeling \[ R_\mathrm{eq}=R_1+R_2\qquad\text{bij serieschakeling}\]
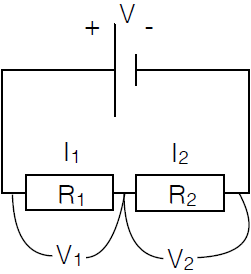
Wanneer twee weerstanden in een elektrisch circuit in serie geplaatst worden, zoals in onderstaand diagram, dan is er in elke component een potentiaalverval gegeven door de wet van Ohm \(V_R=I\cdot R\). De som van de twee spanningsverschillen is gelijk aan de bronspanning \(V\) geleverd door de batterij. In formulevorm \[V=V_1+V_2\] Er kan zich in het circuit geen lading op een plek ophopen en dus is de stroomsterkte overal in het circuit gelijk: \[I=I_1=I_2\] Deze twee vergelijkingen leveren samen op: \[IR = V = V_1+V_2= I_1R_1+I_2R_2 = IR_1+IR_2=I(R_1+R_2)\] Dus: \[R=R_1+R_2\] De in serie geschakelde weerstanden kunnen dus vervangen worden door één weerstand \(R_{\mathrm{eq}}\) waarvan de waarde gelijk is aan de som van de in serie geplaatste weerstanden.
Vervangingsweerstand bij parallelschakeling \[\frac{1}{R_\mathrm{eq}}=\frac{1}{R_1}+\frac{1}{R_2}\qquad\text{bij parallelschakeling}\]
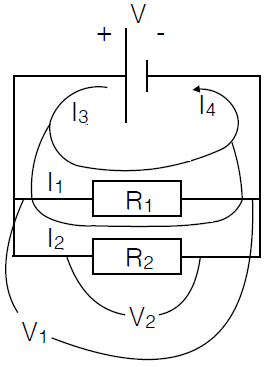
Twee weerstanden die parallel geschakeld zijn en verbonden zijn met geleidende draad met de uiteinden van een batterij, zoals in onderstaand diagram, hebben eenzelfde potentiaalverschil dat de batterij levert. Er geldt dus \[V=V_1=V_2\] De stroom \(I_3\) splitst echter in twee takken, namelijk \(I_1\) en \(I_2\), en komt later weer samen in één stroom \(I_4\). Omdat er geen ophoping van lading kan ontstaan moet gelden: \[I_3=I_4=I_1+I_2\] Laten we \(I_3=I_4\) simpelweg aanduiden met \(I\) en de te berekenen vervangingsweerstand met \(R_{\mathrm{eq}}\) aanduiden, dan kunnen we de wet van Ohm gebruiken om de vergelijking \(I=I_1+I_2\) te herschrijven als \[\frac{V}{R_{\mathrm{eq}}}=\frac{V_1}{R_1}+\frac{V_2}{R_2}=\frac{V}{R_1}+\frac{V}{R_2}=V\left(\frac{1}{R_1}+\frac{1}{R_2}\right)\] en bij deling door \(V\) krijgen we dan \[\frac{1}{R_{\mathrm{eq}}}=\frac{1}{R_1}+\frac{1}{R_2}\]
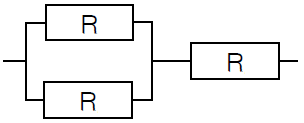
Op welke manier zou je dan met een kleinst mogelijk aantal weerstanden een component in een elektrisch circuit kunnen bouwen met een vervangingsweerstand gelijk aan \(126\,\Omega\)
Bij serieschakeling is de vervangingswaarde gelijk aan de som van de weerstanden.
Bij parallelschakeling is de reciproque waarde van de vervangingswaarde gelijk aan de som van de reciproque waarden van de weerstanden.
De component in een elektrisch circuit met het kleinst mogelijke aantal weerstanden van \(84\,\Omega\) dat een vervangingsweerstand heeft gelijk aan \(126\,\Omega\) bestaat uit 2 parallelle weerstanden die vervolgens in serie staan met één weerstand, zoals in onderstaand diagram met \(R=84\,\Omega\):