Bioelektriciteit: Basisbegrippen
 Elektrische circuits
Elektrische circuits
We hebben al elektrische circuits gezien met een spanningsbron en alleen in serie of parallel geschakelde condensatoren of alleen in serie of parallel geschakelde weerstanden. Maar combinaties van dergelijke elektrische componenten zijn natuurlijk ook toegestaan. Met behulp van de elektriciteitswetten van Kirchhoff kunnen spanningen en stroomsterktes in delen van zo'n algemene stroomkring ook doorgerekend worden.
Stroomwet van Kirchhoff Uit het principe van behoud van elektrische lading volgt:
In elk knooppunt in een elektrische kring is de som van de stromen die in dat punt samenkomen gelijk aan de som van de stromen die vanuit dat punt vertrekken. Het knooppunt kan niet stroom opslaan of afgeven.
Met andere woorden, in elk knooppunt is de algebraïsche som van de stromen (waarbij ingaande stromen positief en uitgaande negatief worden genomen) gelijk aan nul: \[\Bigl(\sum_{\begin{aligned} &k\mathrm{-de\;stroom}\\ &\mathrm{via\;knooppunt}\end{aligned}}I_k \Bigr)= 0\]
Stel dat je een knooppunt \(N\) hebt in een stroomkring zoals in onderstaande figuur.
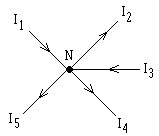
Dan geldt: \[I_1-I_2+I_3-I_4-I_5=0\]
Spanningswet van Kirchhoff Uit het principe van behoud van energie volgt:
De som van de elektrische potentiaalverschillen in elke gesloten lus in een stroomkring is gelijk aan nul.
Hierbij moeten we wel rekening houden met de richting: standaardkeuze is om het potentiaalverschil positief te laten zijn in de richting waar de stroom heengaat en negatief als we een component passeren tegen de richting van de stroom in. Verder is het spanningsverschil over een spanningsbron het tegengestelde van de geleverde spanning.
Met andere woorden, in elke lus is de algebraïsche som van de spanningen (rekening houdend met de richting) gelijk aan nul: \[\Bigl(\sum_{\begin{aligned} &k\mathrm{-de\;component}\\ &\mathrm{in\;lus\;van\;circuit}\end{aligned}}V_k \Bigr)= 0\]
Stel dat je een elektrisch circuit hebt zoals in onderstaande figuur, bestaande uit twee parallel geschakelde weerstanden die op hun beurt in serie geschakeld zijn met een derde weerstand.
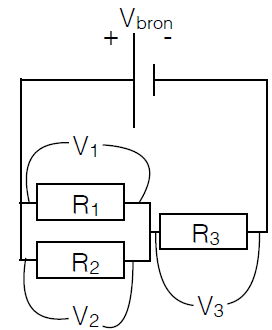
Als we de lus bestaande uit de spanningsbron en weerstanden \(R_1\) en \(R_3\) nemen, dan geeft de spanningswet van Kirchhoff ons \[V_1+V_3-V_\mathrm{bron}=0\] Als we de lus bestaande uit de spanningsbron en weerstanden \(R_2\) en \(R_3\) nemen, dan geeft de spanningswet van Kirchhoff ons \[V_2+V_3-V_\mathrm{bron}=0\] Hieruit volgt ook dat \(V_1=V_2\).
Uitgewerkt voorbeeld van een elektrisch circuit Laten we het laatste voorbeeld eens verder uitwerken. We vullen het plaatje aan met symbolen voor elektrische stromen.
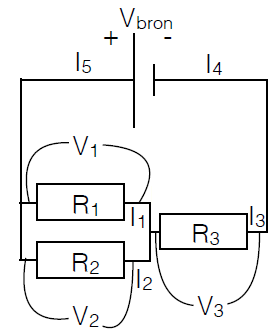
De stroomwet van Kirchhoff geeft de volgende vergelijkingen \[\begin{aligned} I_5-I_1-I_2&=0\\ I_1+I_2-I_3&=0\\ I_3- I_4&=0\\ I_4-I_5&=0\end{aligned}\] Dit kan herschreven worden als \[I_3=I_4=I_5, \qquad I_1+I_2=I_3\]
De spanningswet van Kirchhoff geeft, zoals we eerder gezien hebben, twee vergelijkingen \[V_1+V_3-V_\mathrm{bron}=0, \qquad V_2+V_3-V_\mathrm{bron}=0\] Dit kan herschreven worden als \[V_1=V_2, \qquad V_2+V_3 = V_\mathrm{bron}\]
Verder geldt de wet van Ohm nog voor elke weerstand. Dit geeft nog eens drie vergelijkingen: \[V_1=I_1R_1,\qquad V_2=I_2R_2,\qquad V_3=I_3R_3\]
Door alles samen te nemen krijgen we een stelsel van vergelijkingen. We beschouwen nu de bronspanning \(V_\mathrm{bron}\) en de weerstanden \(R_1\), \(R_2\) en \(R_3\) als parameters waarin de stroomsterktes \(I_1\), \(I_2,\) en \(I_3\) en de spanning \(V_1\), \(V_2\) en \(V_3\) uitgedrukt kunnen worden via algebraïsche formules. Als voorbeeld berekenen we de formule voor \(I_3\).
Uit \[V_1=I_1R_1,\qquad V_2=I_2R_2,\qquad V_1=V_2\] volgt \[I_1R_1=I_2R_2\] Omdat \[I_1=I_3-I_2\] volgt dan \[(I_3-I_2)R_1=I_2R_2\] Dit kan geschreven worden als \[I_3R_1=I_2(R_1+R_2)\] oftewel \[I_2=\frac{I_3R_1}{R_1+R_2}\] Substitutie van deze vergelijking in de vergelijking \[V_\mathrm{bron}=V_2+V_3=I_2R_2+I_3R_3\] geeft \[V_\mathrm{bron}=\frac{I_3R_1R_2}{R_1+R_2}+I_3R_3=I_3\left(R_3+ \frac{R_1R_2}{R_1+R_2}\right)=I_3\left(R_3+\frac{1}{\displaystyle \frac{1}{R_1} +\frac{1}{R_2}}\right) \] Dus \[V_\mathrm{bron}=I_3R_{\mathrm{eq}}\] waarbij de vervangingsweerstand \(R_{\mathrm{eq}}\) voldoet aan \[R_\mathrm{eq}=R_3+\frac{1}{\displaystyle \frac{1}{R_1}+ \frac{1}{R_2}}\] Samengevat \[I_3=\frac{V_\mathrm{bron}}{R_{\mathrm{eq}}}\] met de eerder gegeven formule voor de vervangingsweerstand.
Merk op dat voor dit specifieke circuit de formule voor de vervangingsweerstand veel sneller gevonden had kunnen worden door eerst de parallelle weerstanden \(R_1\) en \(R_2\) te vervangen door een weerstand \(R_{12}\) vastgelegd door de vergelijking \[\frac{1}{R_{12}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}\] oftewel \[R_{12}=\frac{1}{\displaystyle \frac{1}{R_1}+ \frac{1}{R_2}}\] Vervolgens neem je de vervangingsweerstand van in serie geplaatste weerstanden \(R_{3}\) en \(R_{12}\) met als formule \[R_\mathrm{eq}= R_{3}+R_{12}= R_3+\frac{1}{\displaystyle \frac{1}{R_1}+ \frac{1}{R_2}}\]
In het algemeen kun je niet altijd bouwen op de vervangingsregels voor serie- en parallelschakeling. Dit werkt bijvoorbeeld niet bij onderstaand circuit, terwijl de wetten van Kirchhoff hier wel goed blijven functioneren.