Bioelectricity: Core principles
 Charging a capacitor in an RC circuit
Charging a capacitor in an RC circuit
Charging an RC-circuit
We consider an RC circuit, that is, an electric circuit that includes a battery, a resistor, and capacitor in series, with resistance \(R\) and capacitance \(C\), respectively; see the electrical scheme in the following figure. When the switch in the RC circuit is closed at time \(t=0\) (i.e., brought into position A), then the source voltage of the battery, symbolized by \(\mathcal{E}\) which is derived from the more obsolete name electromotive force, drives electrons through the resistor to the plus pole of the battery leaving behind positive charge on the top plate of the capacitor. At the same time, electrons from the negative pole of the battery are driven to the lower plate of the capacitor so that it is negatively charged. When the potential difference across the capacitor, \(V_C\) has become equal to the source voltage of the battery, then the current flow becomes zero. The capacitor plates are then maximally charged. In the figure below we have plotted the normalized charge versus time during the charging of the capacitor.
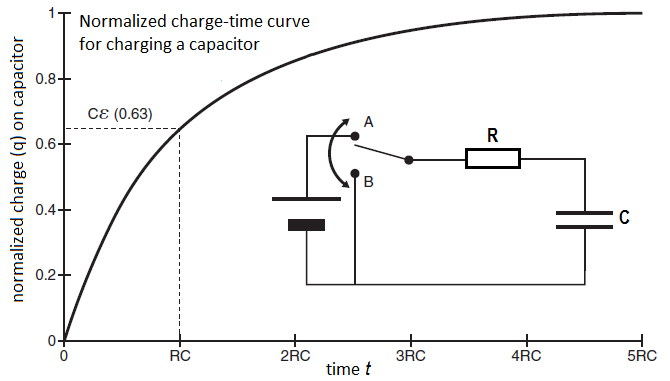
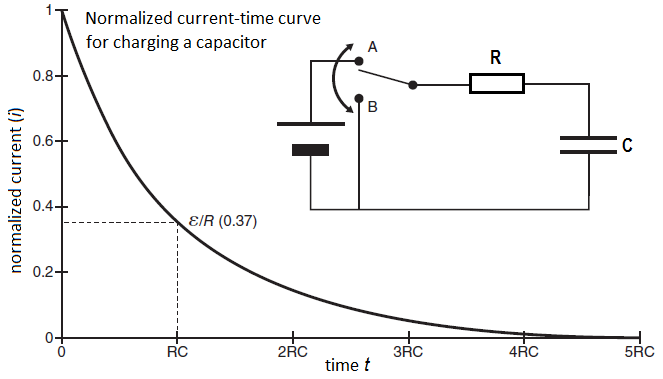
Where the potential of the capacitor increases slowly while charging, the current decreases slowly in the circuit and eventually becomes zero. The figure below shows the normalized current plotted against time during charging of the capacitor.
Derivation of a matching differential equation
The above normalized charge-time and current-time graphs can be mathematically described in precise terms. During the charging process in the RC circuit Kirchhoff's rules apply. The loop rule for voltage states in this case that the voltage drop across the resistor and across the capacitor is equal to the source voltage of the battery. In formula form: \[V_R+V_C=IR+\frac{Q}{C}=\mathcal{E}\] where \(Q(t)\) is the charge of the upper plate of the capacitor at time \(t\) and \(I(t)\) the current in the closed circuit at time \(t\). The current\(I\) is equal to the amount of charge flowing through the circuit per second at any time and is given, by definition, by the following equation: \[I(t) = Q'(t)\] We therefore have the following differential equation: \[R\frac{\dd Q}{\dd t} + \frac{Q}{C} =\mathcal{E}\] or: \[\frac{\dd Q}{\dd t} +\frac{Q}{RC} =\frac{\mathcal{E}}{R}\] This equation can be rewritten as \[\frac{\dd Q}{\dd t} = - \frac{1}{\tau}(Q-\mathcal{E}C)\] with characteristic time \(\tau=RC\). This is a differential equation of limited exponential growth, which can also be written as \[\tau\frac{\dd Q}{\dd t} = \mathcal{E}C - Q\] When the charge no longer changes, that is, when \(\frac{\dd Q}{\dd t}=0\), then the maximum charge \(Q_{\mathrm{max}}\) has been reached. In this case, we have \(\mathcal{E}C - Q_{\mathrm{max}}=0\), that is, \(Q_{\mathrm{max}} = \mathcal{E}C\).
Differential equation for charge in a charging capacitor in an RC circuit An RC circuit is an electric circuit that includes a battery, a resistor, and capacitor in series, with supplied voltage \(\mathcal{E}\), resistance \(R\), and capacitance \(C\), respectively. The differential equation for charge in a charging capacitor in an RC circuit is \[\tau\frac{\dd Q}{\dd t} = Q_{\mathrm{max}}- Q\] with characteristic time \(\tau=RC\) and maximum charge \(Q_{\mathrm{max}}=\mathcal{E}C\). This is a differential equation of limited exponential growth and the solution of this differential equation with \(Q(0)=0\) is \[Q(t) = Q_{\mathrm{max}}\left(1-e^{{}^{-\frac{t}{\tau}}}\right)\]
For the math enthusiast, we determine the explicit solution of the differential equation, written in the form \[\frac{\dd Q}{\dd t} +\frac{Q}{\tau} =\frac{Q_{\mathrm{max}}}{\tau}\] Multiplication of the left- and right-hand side by \(e^{{}^{\frac{t}{\tau}}}\) gives \[\frac{\dd Q}{\dd t}e^{{}^{\frac{t}{\tau}}} +\frac{Q}{\tau}e^{{}^{\frac{t}{\tau}}} =\frac{Q_{\mathrm{max}}}{\tau}e^{{}^{\frac{t}{\tau}}}\] The left-hand side is, because of the product rule for differentiation, equal to a known derivative and the right-hand side can be written as a derivative as well: \[\frac{\dd}{\dd t}\left(Qe^{{}^{\frac{t}{\tau}}}\right) = \frac{\dd}{\dd t}\left(Q_{\mathrm{max}}e^{{}^{\frac{t}{\tau}}}\right)\] So: \[Qe^{{}^{\frac{t}{\tau}}}=Q_{\mathrm{max}}e^{{}^{\frac{t}{\tau}}}+\textit{constant}\] The constant follows from the fact that \(Q(0)=0\) and therefore we get: \[Qe^{{}^{\frac{t}{\tau}}}=Q_{\mathrm{max}}e^{{}^{\frac{t}{\tau}}}-Q_{\mathrm{max}}\] This can be rewritten as \[Q(t) = Q_{\mathrm{max}}\left(1-e^{{}^{-\frac{t}{\tau}}}\right)\]
Formulas for normalized charge and current
The normalized charge \(q(t)=\frac{Q(t)}{Q_{\mathrm{max}}}\) is given by \[q(t)=1-e^{{}^{-\frac{t}{\tau}}}\] At time \(t=\tau=RC\) we have \(q(t) = 1-\exp(-1)\approx 0.63\).
\(\phantom{x}\)
We get the formula for the current by taking the derivative of \(Q(t)\): \[I(t)=\frac{\dd Q}{\dd t}=\frac{\dd}{\dd t}\left(Q_{\mathrm{max}}\Bigl(1-e^{{}^{-\frac{t}{\tau}}}\Bigr)\right)=\frac{Q_{\mathrm{max}}}{\tau}e^{{}^{-\frac{t}{\tau}}}\] The normalized current \(i(t)=\frac{\tau}{Q_{\mathrm{max}}}I(t)\) is given by \[i(t)=e^{{}^{-\frac{t}{\tau}}}\] At time \(t=\tau=RC\) we have \(i(t) = \exp(-1)\approx 0.37\).
\(\phantom{x}\)
For the description of the charging of the capacitor, it is thus convenient to introduce the characteristic time for the formulas \(\tau=RC\). The formula for normalized charge and current will then be: \[q(t)=1-e^{{}^{-\frac{t}{\tau}}} \qquad\text{and}\qquad i(t)=e^{{}^{-\frac{t}{\tau}}}\] This characteristic time, also referred to as RC-time due to the presence of the symbols \(R\) and \(C\), will also be useful in the formulas for discharging a capacitor.


