Bioelektriciteit: Basisbegrippen
 Opladen van een condensator in een RC-circuit
Opladen van een condensator in een RC-circuit
Oplading van een RC-circuit
Een elektrisch circuit bestaande uit een batterij en in serie geschakelde weerstand \(R\) en condensator met capaciteit \(C\) heet een RC-circuit; zie het elektrische schema in onderstaand diagrammen. Als de schakelaar in het RC circuit op tijdstip \(t=0\) gesloten wordt (in positie A gebracht wordt), dan zorgt de bronspanning van de batterij, hier aangeduid met het symbool \(\mathcal{E}\) afkomstig van de verouderde naam elektromotorische kracht, voor een stroom van elektronen door de weerstand naar de plus-pool van de batterij met achterlating van positieve lading op de bovenste plaat van de condensator. Tegelijkertijd worden elektronen vanuit de min-pool van de batterij 'gedreven' naar de onderste plaat van de condensator zodat deze negatief geladen wordt. Als het potentiaalverschil over de condensator, \(V_C\), gelijk geworden is aan de bronspanning van de batterij houdt de elektronenstroom op. De lading op de condensatorplaten is dan maximaal. In onderstaande figuur is de genormaliseerde lading uitgezet tegen de tijd tijdens oplading van de condensator.
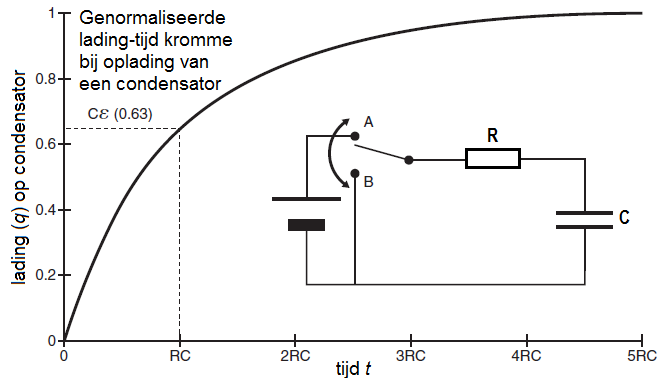
Waar de potentiaal van de condensator langzaam toeneemt tijdens oplading, neemt de stroomsterkte in het circuit langzaam af en wordt uiteindelijk nul. In onderstaande figuur is de genormaliseerde stroomsterkte uitgezet tegen de tijd tijdens oplading van de condensator.
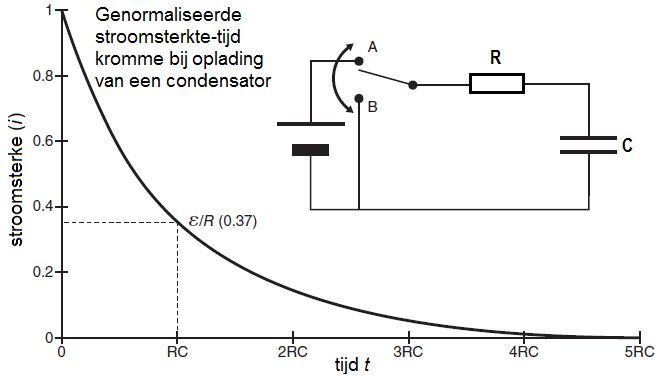
Afleiding van een bijpassende differentiaalvergelijking
Bovenstaande genormaliseerde lading-tijd en stroomsterkte-tijd grafieken kunnen wiskundig exact beschreven worden. Tijdens het opladingsproces gelden voor het RC-circuit de wetten van Kirchhoff. De spanningswet zegt in dit geval dat het spanningsverlies over de weerstand en over de condensator gelijk is aan de bronspanning van de batterij. In formulevorm: \[V_R+V_C=IR+\frac{Q}{C}=\mathcal{E}\] waarbij \(Q(t)\) de lading van de bovenste plaat van de condensator is op tijdstip \(t\) en \(I(t)\) de stroomsterkte in het gesloten circuit is op tijdstip \(t\). De stroomsterkte \(I\) is gelijk aan de hoeveelheid lading dat per seconde op ieder moment door het circuit stroomt en is per definitie gegeven door de volgende vergelijking: \[I(t) = Q'(t)\] We hebben dan ook de volgende differentiaalvergelijking: \[R\frac{\dd Q}{\dd t} + \frac{Q}{C} =\mathcal{E}\] oftewel: \[\frac{\dd Q}{\dd t} +\frac{Q}{RC} =\frac{\mathcal{E}}{R}\] Deze vergelijking is te herschrijven als \[\frac{\dd Q}{\dd t} = - \frac{1}{\tau}(Q-\mathcal{E}C)\] met karakteristieke tijd \(\tau=RC\). DIt is een differentiaalvergelijking van begrensde exponentiële groei, die ook te op te schrijven is als \[\tau\frac{\dd Q}{\dd t} = \mathcal{E}C - Q\] Als de lading niet meer verandert, dat wil zeggen als \(\frac{\dd Q}{\dd t}=0\), dan is de maximale lading \(Q_{\mathrm{max}}\) bereikt. In dit geval moet dan gelden \(\mathcal{E}C - Q_{\mathrm{max}}=0\) oftewel \(Q_{\mathrm{max}} = \mathcal{E}C\).
Differentiaalvergelijking voor lading op een opladende condensator in een RC-circuit Een elektrisch circuit bestaande uit een batterij, die een spanning \(\mathcal{E}\) levert, en in serie geschakelde weerstand \(R\) en condensator met capaciteit \(C\) heet een RC circuit. De differentiaalvergelijking voor lading op een opladende condensator in een RC-circuit is \[\tau\frac{\dd Q}{\dd t} = Q_{\mathrm{max}}- Q\] met karakteristieke tijd \(\tau=RC\) en maximale lading \(Q_{\mathrm{max}}=\mathcal{E}C\). Dit is een differentiaalvergelijking van begrensde exponentiële groei en de oplossing van deze differentiaalvergelijking met \(Q(0)=0\) is \[Q(t) = Q_{\mathrm{max}}\left(1-e^{{}^{-\frac{t}{\tau}}}\right)\]
Voor de liefhebber berekenen we de expliciete oplossing van de differentiaalvergelijking, opgeschreven in de vorm \[\frac{\dd Q}{\dd t} +\frac{Q}{\tau} =\frac{Q_{\mathrm{max}}}{\tau}\] Vermenigvuldiging van linker- en rechterkant van met \(e^{{}^{\frac{t}{\tau}}}\) geeft \[\frac{\dd Q}{\dd t}e^{{}^{\frac{t}{\tau}}} +\frac{Q}{\tau}e^{{}^{\frac{t}{\tau}}} =\frac{Q_{\mathrm{max}}}{\tau}e^{{}^{\frac{t}{\tau}}}\] Het linkerlid is via de productregel voor differentiëren gelijk aan een bekende afgeleide en de rechterkant kunnen we ook als afgeleide schrijven: \[\frac{\dd}{\dd t}\left(Qe^{{}^{\frac{t}{\tau}}}\right) = \frac{\dd}{\dd t}\left(Q_{\mathrm{max}}e^{{}^{\frac{t}{\tau}}}\right)\] Dus geldt: \[Qe^{{}^{\frac{t}{\tau}}}=Q_{\mathrm{max}}e^{{}^{\frac{t}{\tau}}}+\textit{constante}\] De constante volgt uit het gegeven dat \(Q(0)=0\) en dus krijgen we: \[Qe^{{}^{\frac{t}{\tau}}}=Q_{\mathrm{max}}e^{{}^{\frac{t}{\tau}}}-Q_{\mathrm{max}}\] Dit kunnen we herschrijven als \[Q(t) = Q_{\mathrm{max}}\left(1-e^{{}^{-\frac{t}{\tau}}}\right)\]
Formules voor genormaliseerde lading en stroomsterkte
De genormaliseerde lading \(q(t)=\frac{Q(t)}{Q_{\mathrm{max}}}\) wordt dus gegeven door \[q(t)=1-e^{{}^{-\frac{t}{\tau}}}\] Op tijdstip \(t=\tau=RC\) geldt \(q(t) = 1-\exp(-1)\approx 0.63\).
\(\phantom{x}\)
De stroomsterkte krijgen we door de afgeleide te nemen van \(Q(t)\): \[I(t)=\frac{\dd Q}{\dd t}=\frac{\dd}{\dd t}\left(Q_{\mathrm{max}}\Bigl(1-e^{{}^{-\frac{t}{\tau}}}\Bigr)\right)=\frac{Q_{\mathrm{max}}}{\tau}e^{{}^{-\frac{t}{\tau}}}\] De genormaliseerde stroomsterkte \(i(t)=\frac{\tau}{Q_{\mathrm{max}}}I(t)\) wordt dus gegeven door \[i(t)=e^{{}^{-\frac{t}{\tau}}}\] Op tijdstip \(t=\tau=RC\) geldt \(i(t) = \exp(-1)\approx 0.37\).
\(\phantom{x}\)
Bij oplading van de condensator is het voor de formules dus handig de karakteristieke tijd \(\tau=RC\) te introduceren. De formule voor genormaliseerde lading en stroomsterkte worden dan: \[q(t)=1-e^{{}^{-\frac{t}{\tau}}} \qquad\text{en}\qquad i(t)=e^{{}^{-\frac{t}{\tau}}}\] Deze karakteristieke tijd, die vanwege de aanwezige symbolen ook RC-tijd genoemd wordt, zal ook zijn nut bewijzen in de formules voor ontlading van een condensator.


