Ontladen van een condensator in een RC-circuit

Bioelektriciteit: Basisbegrippen

Ontladen van een condensator in een RC-circuit

Ontlading van een RC circuit

We bekijken een elektrisch circuit waarin een condensator met capaciteit $C$ ontlaadt via een weerstand $R$ zoals in het elektrische schema in onderstaand diagram. Eerst stond de schakelaar in stand A zodat de condensator volledig opgeladen kon worden. Hierna wordt de schakelaar in het RC circuit op tijdstip $t=0$ in positie B gebracht, speelt de batterij geen rol meer, en kan de ontlading van de condensator beginnen, met de condensator functionerend als een continue afnemende spanningsbron

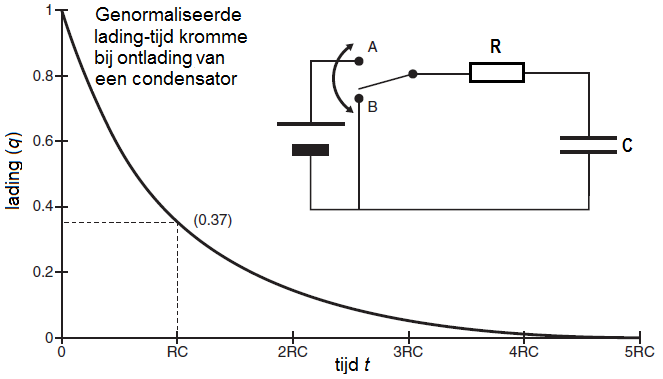
ontlading van een condensator

Afleiding van een bijpassende differentiaalvergelijking

Bovenstaande genormaliseerde lading-tijd grafiek kan wiskundig exact beschreven worden. Tijdens het ontladingsproces gelden voor het RC circuit de wetten van Kirchhoff. De spanningswet zegt in dit geval dat de som van het spanningsverlies over de weerstand en over de condensator gelijk is aan nul. In formulevorm:

$V_R+V_C=IR+\frac{Q}{C}=0$ waarbij $Q(t)$ de lading van de bovenste plaat van de condensator is op tijdstip $t$ en $I(t)$ de stroomsterkte in het gesloten circuit is op tijdstip $t$ . De stroomsterkte $I$ is gelijk aan de hoeveelheid lading die per seconde op ieder moment door het circuit stroomt en is per definitie gegeven door de volgende vergelijking:

$I(t) = Q'(t)$ We hebben dan ook de volgende differentiaalvergelijking:

$R\frac{\dd Q}{\dd t} + \frac{Q}{C} =0$ oftewel:

$\frac{\dd Q}{\dd t} =-\frac{1}{RC}Q$ Dit is de differentiaalvergelijking van exponentieel verval, die geschreven kan worden als

$\frac{\dd Q}{\dd t} = -\frac{Q}{\tau}$ met karakteristieke tijd $\tau=RC$ , ook wel RC-tijd genoemd.

Differentiaalvergelijking voor lading op een ontladende condensator in een RC-circuit

Een elektrisch circuit bestaande uit een in serie geschakelde weerstand $R$ en condensator met capaciteit $C$ , en optioneel een batterij die een spanning $\mathcal{E}$ levert, heet een RC-circuit. Als we geen batterij hebben, is de differentiaalvergelijking voor lading op een ontladende condensator in een RC-circuit gelijk aan

$\frac{\dd Q}{\dd t} = -\frac{1}{\tau}\cdot Q$ met karakteristieke tijd $\tau=RC$ en maximale lading $Q(0)=Q_{0}$ op tijdstip $t=0$ . Dit is een differentiaalvergelijking van exponentieel verval en de oplossing van deze differentiaalvergelijking is

$Q(t) = Q_{0}\cdot e^{{}^{-\frac{t}{\tau}}}$

Voor de liefhebber bewijzen we de expliciete oplossing van de differentiaalvergelijking, opgeschreven in de vorm

$\frac{\dd Q}{\dd t} - \frac{Q}{\tau} =0$ Vermenigvuldiging van linker- en rechterkant van met $e^{{}^{\frac{t}{\tau}}}$ geeft

$\frac{\dd Q}{\dd t}\cdot e^{{}^{\frac{t}{\tau}}} +\frac{Q}{\tau}\cdot e^{{}^{\frac{t}{\tau}}} =0$ Het linkerlid is via de productregel voor differentiëren gelijk aan een bekende afgeleide:

$\frac{\dd}{\dd t}\left(Q\cdot e^{{}^{\frac{t}{\tau}}}\right) = 0$ Dus geldt:

$Q\cdot e^{{}^{\frac{t}{\tau}}}=\textit{constante}$ De constante volgt uit het gegeven dat $Q(0)=Q_{0}$ en dus krijgen we:

$Q\cdot e^{{}^{\frac{t}{\tau}}}=Q_{0}$ Dit kunnen we herschrijven als

$Q(t) = Q_{0}\cdot e^{{}^{-\frac{t}{\tau}}}$

Formules voor genormaliseerde lading en stroomsterkte

De genormaliseerde lading $q(t)=\frac{Q(t)}{Q_0}$ wordt dus gegeven door

$q(t)=e^{{}^{-\frac{t}{\tau}}}$ Op tijdstip $t=\tau$ geldt $q(\tau) = \exp(-1)\approx 0.37$ .

$\phantom{x}$

De stroomsterkte krijgen we door de afgeleide te nemen van $Q(t)$ :

$I(t)=\frac{\dd Q}{\dd t}=\frac{\dd}{\dd t}\left(Q_0e^{{}^{-\frac{t}{\tau}}}\right)=\frac{Q_0}{\tau}e^{{}^{-\frac{t}{\tau}}}$ De genormaliseerde stroomsterkte $i(t)=\frac{\tau}{Q_0}I(t)$ wordt dus gegeven door

$i(t)=e^{{}^{-\frac{t}{\tau}}}$ Op tijdstip $t=\tau$ geldt $i(t) = \exp(-1)\approx 0.37$ .

De tijdgrafieken van genormaliseerde lading en stroomsterkte zijn dus dezelfde exponentiële vervalkromme. Omdat de lading op een condensatorplaat evenredig is met de spanning geldt dit ook voor de genormaliseerde spanning over de condensator.