Diffusion

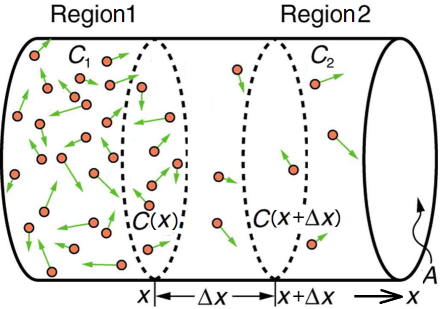
Physical chemistry teaches us that there is a movement of ions from areas of high to low concentration, and that the flux \(\Phi\), that is, the net movement of ions per unit time per unit surface region in the direction of the decreasing concentration, is given by Fick's law: \[\Phi= -D\cdot \frac{\dd C}{\dd x}\] where \(D\) is the diffusion coefficient and \(\dfrac{\dd C}{\dd x}\) is the component of the gradient of the concentration that points in the direction in which the transport (local) is happening (in the drawing below the positive \(x\) direction). The minus sign takes into account that the direction of transport is from areas with a high concentration to areas of low concentration. The figure below illustrates this process and the formula \[\Phi(x)\cdot \Delta x \approx -D\cdot \bigl(C(x+\Delta x)-C(x)\bigr)\] symbolizes that the number of particles that flows into the volume between \(x\) and \(x+\Delta x\) per unit of time is proportional to the concentration difference between the locations \(x\) and \(x+\Delta x\) at that time.

Einstein and Nernst have derived the following formula for the diffusion constant of a charged particle: \[D=\frac{RT}{F}\cdot u\] where \(R\) is the gas constant, \(T\) the absolute temperature (in Kelvin), \(F\) the Faraday constant (the charge of one mole of monovalent ions) and \(u\) the 'mobility' of the ion. When one mole of ions with valence \(z\) (the number of unit charges per ion) diffuses we can interpret this as an electric flow corresponding with the current \[I_D= zF\cdot \Phi = - zRT\cdot u\cdot \frac{\dd C}{\dd x} \]

Movement of ions in an electric field

The diffusion of ions from a region of high concentration to a region of low concentration, which are separated from each other by a semipermeable membrane, results in a charge difference near the membrane. Suppose that the ion is positively charged, has a high concentration within the cell, and has a low concentration outside the cell, then diffusion causes that negative charge remains on the inside of the membrane and that outside the cell near the membrane positive charge accumulates. The membrane is in this way a capacitor and as more ions diffuse this charge difference increases. But this also means that there is an increasing potential difference in the vicinity of the membrane. The diffusion of the ions will therefore become increasingly more difficult because of opposing electrical forces. The flux \(\Phi_E\) as a result of the electric field \(E\) that corresponds with the potential difference \(V\) is given by the following formula: \[\Phi_E=-z\cdot u\cdot C\cdot \frac{\dd V}{\dd x}\] where \(z\) again is the valence of the ion and \(\dfrac{\dd V}{\dd x}\) is the potential difference per distance. When one mole of particles having valence \(z\) moves in the electric field, we can interpret this as an electric flow with a current \[I_E=zF\cdot\Phi_E = -z^2F\cdot u\cdot C\cdot \frac{\dd V}{\dd x}\]

The Nernst equation

There establishes little by little an equilibrium in which the diffusion and the movement of the ions in an electric field have the same size, but are oppositely directed; we say that the cell is 'at rest', but there actually is movement of ions through the membrane, but the inflow and outflow are equal to each other. In other words, in equilibrium, the sum of the electric current because of diffusion and movement of ions in an electric field, \(I_D+I_E\), is equal to zero. So \[I_D+I_E = -z\cdot u\cdot \!\!\left(RT\cdot \frac{\dd C}{\dd x}+zFC\cdot \frac{\dd V}{\dd x}\right)=0\] In equilibrium, the term between brackets must be equal to zero, and this gives: \[-\frac{RT}{zF}\cdot \frac{1}{C}\cdot \frac{\dd C}{\dd x}= \frac{\dd V}{\dd x}\] This implies: \[-\frac{RT}{zF}\cdot \frac{\dd\ln(C)}{\dd x}= \frac{\dd V}{\dd x}\] Therefore, when we integrate over the lipid bilayer and apply the rule \(\ln(x)-\ln(y)=\ln(x/y)\), then we get \[-\frac{RT}{zF}\ln\left(\frac{C_\mathrm{e}}{C_\mathrm{i}}\right)=V_\mathrm{e}-V_\mathrm{i}\] So: \[V_\mathrm{i}-V_\mathrm{e}= \frac{RT}{zF}\ln\left(\frac{C_\mathrm{e}}{C_\mathrm{i}}\right)\] On the left-hand side we have a potential difference between the interior and exterior of the membrane for a cell at rest, but in electrophysiology it is common practice to set the reference potential on the outside of the cell near the membrane equal to zero. For a positively charged ion with a higher concentration on the inside of the cell at rest, the potential will then have on the inside of the cell near the membrane a negative value, which we call the Nernst potential or equilibrium potential of the ion and denote by \(E_\mathrm{ion}\). The equation found is called the Nernst equation.